Varianzanalyse mit Messwiederholung
Johannes Lüken / Dr. Heiko Schimmelpfennig
Wenn eine Person Bewertungen zu verschiedenen Objekten – beispielsweise Marken – abgibt oder bei ihr Erhebungen zu mehreren Zeitpunkten erfolgen, sind die Messwerte voneinander abhängig. Ob sich die zweiten Messungen einer Variable signifikant von den ersten unterscheiden, kann mit einem t-Test für abhängige Stichproben überprüft werden. Liegen Messwerte zu mehr als zwei Zeitpunkten vor, wird eine Varianzanalyse mit Messwiederholung eingesetzt. Um den Vorteil dieser Verfahren gegenüber der Anwendung des konventionellen t-Tests für unverbundene Stichproben oder der Varianzanalyse ohne Messwiederholung in dieser Situation zu verdeutlichen, genügt die Betrachtung von zwei Messzeitpunkten.
Vergleich des t-Tests für abhängige und unverbundene Stichproben
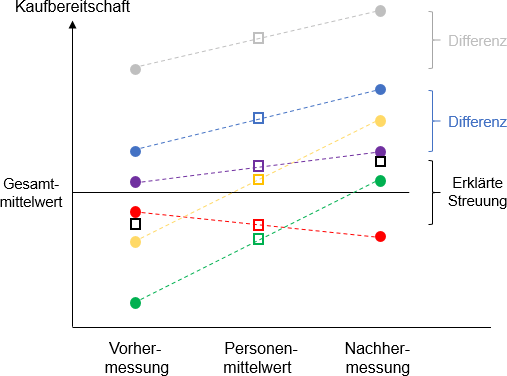
Es wird die Kaufbereitschaft vor und unmittelbar nach dem Ausprobieren eines Produktes erhoben. Die gefüllten Kreise in der Abbildung zeigen die Messergebnisse. Die zu einer Person gehörenden Werte sind jeweils durch dieselbe Farbe gekennzeichnet.
Abbildung: Ergebnisse von Vorher-und Nachhermessung für sechs Personen
Hat sich die Kaufbereitschaft von Vorher- zu Nachhermessung signifikant verändert? Bei Anwendung des t-Tests für unverbundene Stichproben stellen die Vorhermessungen Werte der einen und die Nachhermessungen Werte der anderen Gruppe dar. Es wird untersucht, ob sich die Mittelwerte der beiden Gruppen signifikant unterscheiden. Beim t-Test für abhängige Stichproben wird für jedes Wertepaar die Differenz berechnet und überprüft, ob der Mittelwert der Differenzen signifikant von null abweicht.
Für die Messwerte (a) der fünf „bunten“ Personen und (b) derselben Personen nur mit der „grauen“ anstelle der „blauen“ Person ist der Unterschied der Mittelwerte von Vorher- und Nachhermessungen gleich hoch. Aufgrund der geringeren Standardabweichung der Werte in (a) ist der Unterschied bei Anwendung des t-Tests für unverbundene Stichproben eher statistisch signifikant als in (b). Das Ergebnis des t-Tests für abhängige Stichproben ist dagegen für (a) und (b) trotz unterschiedlicher Standardabweichung der Rohwerte identisch, da die graue und die blaue Differenz gleich sind. Im Allgemeinen besitzt der t-Test für abhängige Stichproben unter gleichen Bedingungen eine höhere Power als der für unverbundene Stichproben. Das heißt, die Wahrscheinlichkeit einen tatsächlich vorliegenden Unterschied zu entdecken, ist höher.
Einfaktorielle Varianzanalyse mit Messwiederholung
Die Streuung aller Messwerte um den Gesamtmittelwert kann aufgeteilt werden in
- die Streuung der Mittelwerte der Vorher- und Nachhermessung (● für die fünf „bunten“ Personen) um den Gesamtmittelwert = durch das Ausprobieren des Produktes erklärte Streuung,
- die Streuung der Personenmittelwerte um den Gesamtmittelwert = erklärte Streuung zwischen den Personen und
- die restliche Streuung = nicht erklärte Streuung.
Je größer das Verhältnis aus durch das Ausprobieren erklärter Streuung und nicht erklärter Streuung ist, desto eher zeigt sich ein signifikanter Unterschied der Mittelwerte der Vorher- und Nachhermessung. Im Fall von zwei Messzeitpunkten ergibt sich das gleiche Ergebnis wie beim t-Test für abhängige Stichproben.
Im Vergleich zu einer Varianzanalyse ohne Messwiederholung, in der Vorher- und Nachhermessung zwei unverbundene Gruppen sind, ist die erklärte Streuung durch das Ausprobieren gleich hoch, die nicht erklärte Streuung aufgrund der zusätzlich erklärten Streuung zwischen den Personen jedoch geringer. Insofern ist das Verhältnis aus erklärter und nicht erklärter Streuung bei der Varianzanalyse mit Messwiederholung größer als das ohne Messwiederholung. Erstere besitzt eine höhere Power.
Varianzanalyse mit Messwiederholung für 3 oder mehr Messungen
Falls nach längerem Ausprobieren eine weitere Erhebung der Kaufbereitschaft erfolgt, liegen für jede Person drei Werte vor, über die die Personenmittelwerte berechnet werden. Die Aufteilung der Streuung aller Messwerte und das Prinzip des Tests ändern sich nicht. Gibt es einen signifikanten Effekt des Ausprobierens, kann anhand von Post-hoc-Tests geklärt werden, ob zwischen der ersten und zweiten, der ersten und dritten und/oder der zweiten und dritten signifikante Unterschiede bestehen.
Beitrag aus planung&analyse 17/4 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Eid, M.; Gollwitzer, M.; Schmitt, M. (2013): Unterschiede zwischen mehreren abhängigen Stichproben: Varianzanalyse mit Messwiederholung und verwandte Verfahren. In: Statistik und Forschungsmethoden, 3. Auflage, Weinheim, Basel, 2013, S. 446-493.
Lüken, J.; Schimmelpfennig, H. (2016): Mittelwertvergleiche mittels t-Test. In: planung&analyse, Nr. 2/2016, S. 65.
<