
Treiberanalyse mit Entscheidungsbäumen
Johannes Lüken / Dr. Heiko Schimmelpfennig
Random Forests sind nicht nur zur Prognose, sondern zugleich zur Analyse der Treiber einer abhängigen Variable einsetzbar. Gegenüber vielen anderen Verfahren besitzen sie den Vorteil, dass mühelos Treiber mit unterschiedlichen Skalenniveaus untersucht werden können und keine Annahme über die Form des Zusammenhangs zur abhängigen Variable getroffen wird. Zudem stellt Multikollinearität für sie kein Problem dar. Je nach Skalenniveau der abhängigen Variable existieren mehrere Möglichkeiten zur Messung der Bedeutung der Treiber, von denen eine anhand eines aktuellen Beispiels näher vorgestellt wird.
Treiber des Erfolgs bei der Fußball-WM 2018
Es wurden die auf kicker.de zur Verfügung stehenden Angaben zu Ballbesitz (in %), Anzahl Torschüsse, Passquote (in %), Zweikampfquote (in %) und Anzahl Standards (= Summe aus Frei-/strafstößen und Ecken) der 48 Spiele der Gruppenphase der Fußball-WM 2018 erfasst. Beantwortet werden soll die Frage, welcher von diesen der wichtigste Faktor für einen Sieg ist.
Ein mögliches Trennungskriterium zur Induktion eines Entscheidungsbaums ist der Gini-Index. Er misst die „Unreinheit“ eines Knotens. Allgemein ist er für m Kategorien der abhängigen Variable definiert durch
Gk = p1 · (1-p1) + p2 · (1-p2) + ··· + pm · (1-pm)
mit p = Anteil einer Kategorie in einem Knoten k.
Bei einer Gleichverteilung über die Kategorien nimmt der Gini-Index mit 0,5 sein Maximum an. Er ist umso geringer, je eindeutiger eine Kategorie in einem Knoten ausgeprägt ist. Über alle Spiele der Gruppenphase hinweg verließen 41% aller Teams den Platz als Sieger. Insofern beträgt er im ersten Knoten des Entscheidungsbaums in der Abbildung G1 = 0,41 (1-0,41) + 0,59 · (1-0,59) = 0,48.
Es wird jeweils diejenige Variable für die Trennung ausgewählt, mit der der Gini-Index am meisten verringert werden kann. In dem Beispiel ist dies als erstes die Zweikampfquote. Von den Teams, die mindestens 52% der Zweikämpfe gewannen, siegten 67%. Von den Teams mit einer geringeren Zweikampfquote siegten nur 27%. Im zweiten Knoten ist somit G2 = 0,27 (1-0,27) + 0,73 · (1-0,73) = 0,39 und im dritten G3 = 0,67 (1-0,67) + 0,33 · (1-0,33) = 0,44. Damit verbessert sich der Gini-Index durch diesen Split um G1 – (Anteil des Knotens 2 am Knoten 1) G2 – (Anteil des Knotens 3 am Knoten 1) G3 = 0,48 – 0,66 0,39 – 0,34 0,44 = 0,07. Da Variablen in einem Entscheidungsbaum mehr als einmal als Trennungsvariable genutzt werden können (siehe Zweikpampfquote), ist die Bedeutung eines Treibers durch die Summe aller der durch diesen bedingten Verbesserungen bestimmt.
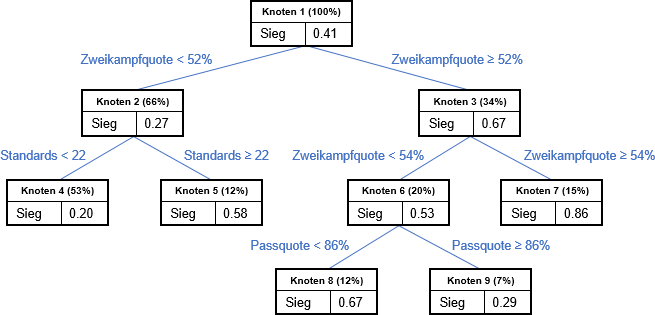
Abbildung: Ausschnitt aus einem mit CART erzeugten Entscheidungsbaum
Analog zu der Idee, eine Prognose nicht auf einen einzigen Baum zu stützen, wird mittels Random Forest ein Ensemble an Entscheidungsbäumen erzeugt. Schließlich entspricht die Bedeutung eines Treibers dem Mittelwert der Summe der Verbesserungen über alle Bäume. Bei 1000 Bäumen betragen die auf eine Summe von 100% normierten Wichtigkeiten der Treiber für einen Sieg: Zweikampfquote = 26%, Anzahl Torschüsse = 21%, Anzahl Standards = 19%, Ballbesitz = 18%, Passquote = 16%.
Das Ergebnis ist jedoch nicht eindeutig. Es hängt ein wenig ab von der Startlösung und ein wenig mehr von der vorgegebenen Anzahl an Variablen (hier: 2), die bei jedem Split zufällig als Kandidaten für die Trennungsvariable ausgewählt werden. Falls die Kandidaten unterschiedliche Skalenniveaus besitzen, werden zudem die mit mehr Kategorien als Trennungsvariable bevorzugt. Vor diesem Hintergrund ist es empfehlenswerter, das Ergebnis nur als Rangfolge zu interpretieren.
Alternative Messungen der Bedeutung von Treibern
Für jeden mittels Random Forest erzeugten Baum wird generell nur ein Teil des untersuchten Datensatzes verwendet. Die Trefferquote für den anderen Teil ist Ausgangspunkt einer alternativen Messung der Bedeutung eines Treibers einer kategorialen Variable. Diese wird mit der Trefferquote verglichen, die sich ergibt, wenn die Ausprägungen des betrachteten Treibers zufällig vertauscht werden. Verringert sie sich kaum, sind die Ausprägungen des Treibers im Grunde egal und seine Bedeutung dementsprechend gering. Verringert sich die Trefferquote sehr, besitzt der Treiber eine hohe Bedeutung. Die endgültige Bedeutung entspricht dann dem Mittelwert der Verschlechterungen über alle Bäume.
Bei metrischen abhängigen Variablen können die Ansätze ebenso genutzt werden – nur, die verwendeten Maße basieren dann auf den Residuen.
Beitrag aus planung&analyse 18/5 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Breiman, L.: Manual on Setting Up, Using, and Understanding Random Forests V3.1, 2002, http://oz.berkeley.edu/users/breiman/Using_random_forests_V3.1.pdf.
Eberl, M. et al.: Treiberanalysen im Fitness-Check. In: planung&analyse, Nr. 6/2015, S. 39-43.
Grömping, U.: Variable Importance Assessment in Regression: Linear Regression versus Random Forest. In: The American Statistician, Nr. 4/2009, S. 308-319.
<






