Total Unduplicated Reach and Frequency (TURF)

Johannes Lüken / Dr. Heiko Schimmelpfennig

Total Unduplicated Reach (Nettoreichweite) und Frequency (Frequenz) sind Kennzahlen, die aus der Mediaplanung stammen. Eine TURF-Analyse nutzt sie insbesondere zur Unterstützung von Entscheidungen über das Produktprogramm oder das Sortiment. Eingesetzt werden sie beispielsweise, um die richtige Auswahl an Farben, Düften oder Geschmacksrichtungen zu treffen.

Nettoreichweite und Frequenz

Die Nettoreichweite ist die Anzahl oder der Anteil der Personen in einer Stichprobe, die zumindest ein Produkt eines Sortiments bzw. eine Variante einer Produktlinie kaufen würden. Die Frequenz entspricht der Anzahl der Produkte eines Sortiments bzw. Varianten einer Produktlinie, die eine Person kaufen würde, summiert über alle Personen der Stichprobe.

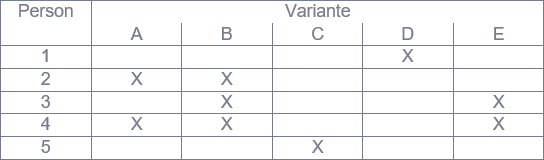
In dem Datenbeispiel aus Abbildung 1 stehen fünf Produktvarianten zur Auswahl. Die „X“ in einer Zeile repräsentieren die Varianten, die für eine Person – ermittelt zum Beispiel durch eine Befragung – für einen Kauf infrage kommen. Für eine einzelne Variante sind Nettoreichweite und Frequenz identisch. Besteht die Produktlinie beispielsweise lediglich aus Variante A, so sind beide in dem Beispiel gleich zwei (Person 2 und 4). Eine Produktlinie mit den Varianten A und B weist eine Nettoreichweite von drei (Person 2, 3 und 4) sowie eine Frequenz von fünf auf.

Abbildung 1: Kaufbereitschaft für fünf Produktvarianten

Ziel einer TURF-Analyse

Die TURF-Analyse will für vorgegebene Umfänge des Sortiments oder der Produktlinie die Kombination von Produkten oder Varianten finden, welche die Nettoreichweite bzw. die Frequenz maximiert. Die Kombination mit der höchsten Frequenz ist einfach zu finden. Es sind die Produkte oder Varianten mit der für sich allein betrachtet größten Frequenz. Um die Kombination mit der höchsten Nettoreichweite zu bestimmen, sind alle möglichen Kombinationen zu untersuchen. Für einen vorgegebenen Umfang k des Sortiments oder der Produktlinie sind dies bei n zur Auswahl stehenden Produkten oder Varianten n!/(k!×(n-k)!) Möglichkeiten, wobei n! = n×(n-1)×(n-2)× ××× ×1. Beispielsweise sind bei einer Auswahl von 15 aus 50 Varianten über zwei Billionen verschiedene Produktlinien denkbar. Um bei Problemstellungen dieser Größenordnungen in akzeptabler Zeit ein Ergebnis zu erhalten, ist eine intelligente Suche erforderlich, die nicht alle möglichen Kombinationen betrachten muss (siehe dazu Bausch/Schimmelpfennig, 2012).

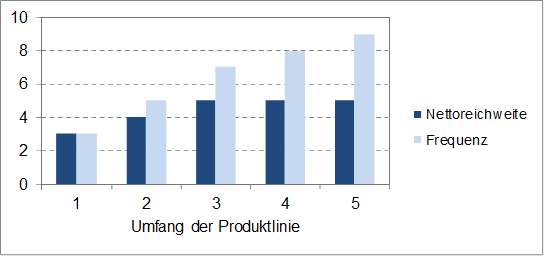
Abbildung 2 veranschaulicht für das Datenbeispiel die Entwicklung der maximalen Werte der beiden Kennzahlen in Abhängigkeit vom Umfang der Produktlinie. Mit einer Produktlinie bestehend aus den drei Varianten B, C und D wird bereits eine Nettoreichweite von fünf (gleich 100%) erzielt. Das heißt für alle Personen in der Stichprobe ist unter den Varianten B, C und D zumindest eine, die sie kaufen würden. Eine Erweiterung der Produktlinie auf vier oder fünf Varianten ist hinsichtlich der Nettoreichweite insofern unnötig. Für drei Varianten besitzen die Varianten A, B und E mit sieben die höchste Frequenz. Falls von einer Person aber nur jeweils eine Variante gekauft wird, bedeutet diese Zusammensetzung drei und nicht fünf verkaufte Produkte wie bei den drei Varianten mit der höchsten Nettoreichweite. Die Frequenz ist als Optimierungskriterium eher dann interessant, wenn nach der üblicherweise gekauften Anzahl beispielsweise von Joghurts pro Woche gefragt wird und diese auf verschiedene Sorten zu verteilen ist.

Abbildung 2: Maximale Nettoreichweite und Frequenz

MaxDiff, Conjoint-Analyse und TURF

Bei einem MaxDiff können Produktvarianten oder Features von Produkten Gegenstand der Erhebung sein. Bei der Conjoint-Analyse sind es Produktvarianten, die sich aus Ausprägungen mehrerer Eigenschaften zusammensetzen. Ergebnisse sind jeweils Nutzenwerte, die die Präferenzen der Befragten widerspiegeln. Diese können mit einer TURF-Analyse weiter ausgewertet werden, um Pakete von Features zu definieren, so dass für möglichst viele mindestens eins darin wichtig ist, oder um aus der Vielzahl an denkbaren Produktvarianten eines Conjoints eine Produktlinie mit der höchsten Nettoreichweite zu finden.

Dazu ist eine Dichotomisierung der Nutzenwerte notwendig, um wie in dem Datenbeispiel zwischen infrage und nicht infrage kommenden Varianten oder wichtigen und unwichtigen Features zu unterscheiden. Im MaxDiff bedarf es dazu zusätzlicher Fragen. Werden Features von Produkten beurteilt, sind von den Befragten die wichtigen Features explizit anzugeben (Durchführung eines Anchored MaxDiff). Werden Produktvarianten betrachtet, sind für die am häufigsten als beste und als schlechteste ausgewählten Varianten Kaufwahrscheinlichkeiten p_b(est) und p_w(orst) zu erheben. Dann lässt sich der Nutzenwert u jeder Variante unter Annahme eines linearen Zusammenhangs in eine Kaufwahrscheinlichkeit p gemäß p = p_w + (u-u_w)×(p_b-p_w)/(u_b-u_w) umrechnen. Schließlich ist ein Grenzwert für die Kaufwahrscheinlichkeit festzulegen, ab dem davon ausgegangen werden kann, dass eine Variante gekauft wird. Analog kann in der Conjoint-Analyse vorgegangen werden, wenn in der Befragung im Anschluss an das Conjoint für zwei möglichst unterschiedliche Produkte Kaufwahrscheinlichkeiten abgefragt werden. Ferner ermöglichen Conjoint-Analysen wie das Choice Based Conjoint (CBC), die für jeden Befragten den Nutzenwert einer „Nicht-Kauf-Option“ schätzen, anhand dieses Wertes zwischen infrage und nicht infrage kommenden Produktvarianten zu trennen. TURF-Analysen können somit den praktischen Nutzen von MaxDiff- und Conjoint-Analysen noch weiter steigern.

Beitrag aus planung&analyse 14/5 in der Rubrik „Statistik kompakt“

Autoreninformation

Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.

Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.

Literatur

Adler, T.J.; Smith, C.; Dumont, J.: Optimizing Product Portfolios Using Discrete Choice Modeling and TURF. In: Hess, S.; Daly, A. (Hrsg.): Choice-Modelling: The State-of-the-Art and the State-of-Practice, Bingley, 2010, S. 485-497.

Bausch, T.; Schimmelpfennig, H.: TURF auf der Überholspur. In: planung & analyse, Jg. 39/2012, Nr. 3, S. 62-65.

Cohen, E.: TURF analysis. In: Quirk’s Marketing Research Review, July/August 1993, S. 10-13.

Zurück zur Übersicht

Share