Strukturgleichungs-Modellierung

Johannes Lüken / Dr. Heiko Schimmelpfennig

Die Strukturgleichungsmodellierung zählt zu den bedeutendsten Methoden der Kausalanalyse. Sie erweitert die multiple Regressionsanalyse in zweifacher Hinsicht: Zum einen ist es möglich, nicht nur Vermutungen über kausale Zusammenhänge mehrerer unabhängiger und lediglich einer abhängigen Variable, sondern auch über komplexere Zusammenhänge zwischen Variablen zu überprüfen. Zum anderen erlaubt sie, nicht unmittelbar beobachtbare – so genannte latente – Variablen wie Einstellung, Involvement oder Loyalität zu berücksichtigen.

Bestandteile eines Strukturgleichungsmodells

Üblicherweise werden die vermuteten Zusammenhänge zwischen den Variablen in einem Pfaddiagramm grafisch veranschaulicht (siehe Abbildung).

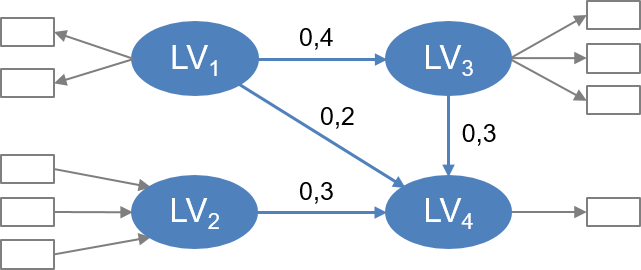
Abbildung: Beispiel eines Strukturgleichungsmodells

Latente Variablen (LV) werden durch Ellipsen gekennzeichnet. Gemeinsam mit den Pfeilen, die zeigen, welche latenten Variablen sich beeinflussen, bilden sie das Strukturmodell. Da eine latente Variable sowohl andere bestimmen als auch von anderen bestimmt werden kann, wird nicht zwischen unabhängigen und abhängigen, sondern zwischen exogenen und endogenen latenten Variablen differenziert. Diejenigen, die von keiner latenten Variable beeinflusst werden, sind exogen (in der Abbildung LV₁ und LV₂). Die übrigen sind endogen (in der Abbildung LV₃ und LV₄).

Zur Messung einer latenten Variable bedarf es eines oder mehrerer Indikatoren, die direkt beobachtbar sind. Diese werden im Pfaddiagramm als Rechtecke dargestellt. Die jeweils zu einer latenten Variable gehörenden Indikatoren bilden ihr Messmodell. Grundlegend ist die Unterscheidung zwischen reflektiven und formativen Messmodellen. Einem reflektiven Messmodell liegt die Annahme zugrunde, dass die latente Variable verantwortlich für die Ausprägungen der Indikatoren ist (in der Abbildung zum Beispiel LV₁: die Pfeile zeigen von der latenten Variable auf die Indikatoren). In einem formativen Messmodell machen die Indikatoren zusammen die latente Variable aus (in der Abbildung LV₂: die Pfeile zeigen von den Indikatoren auf die latente Variable). Ein plakatives Beispiel ist die Messung von Trunkenheit: Diese kann reflektiv zum Beispiel durch den Atemalkohol und die Fähigkeit, auf einer geraden Linie entlang gehen zu können, oder aber formativ durch die konsumierten Mengen an Bier, Wein etc. gemessen werden. Unterschieden werden zwei Arten formativer Messmodelle: die beobachteten Indikatoren bestimmen die latente Variable entweder a) vollständig oder b) nur zu einem Teil. Wird angenommen, dass Trunkenheit durch die Mengen der verschiedenen Alkoholika vollständig erfasst ist, wird die latente Variable durch diese Indikatoren auch inhaltlich eindeutig definiert: die Gesamtmenge des Alkoholkonsums. Geht die inhaltliche Bedeutung einer Definition des Begriffs „Trunkenheit“ aber darüber hinaus, so würde sie durch die konsumierten Mengen nur unvollständig gemessen.

Schätzverfahren

Zur Schätzung der Pfadkoeffizienten, das heißt der Stärke der Einflüsse der latenten Variablen aufeinander, sowie der Beziehungen zwischen den latenten Variablen und ihren Indikatoren haben sich zwei Ansätze etabliert: die Kovarianzstrukturanalyse und das Partial-Least-Squares-(PLS-)Verfahren. Die Kovarianzstrukturanalyse, die auch unter der Bezeichnung LISREL (Linear Structural Relationships) geläufig ist, betrachtet ein Strukturgleichungsmodell als Ganzes. Sie bestimmt die Koeffizienten so, dass die Kovarianzen der Indikatoren möglichst gut mit den aufgrund der geschätzten Koeffizienten reproduzierten Kovarianzen übereinstimmen. Im Gegensatz zur Kovarianzstrukturanalyse zerlegt PLS das Gesamtmodell in Teilmodelle von unmittelbar im Modell zusammenhängenden Variablen und berechnet Fallwerte für die latenten Variablen. Die Pfadkoeffizienten werden dann durch multiple Regressionen bestimmt, in denen jeweils eine endogene latente Variable die abhängige Größe ist. Eng verwandt mit PLS ist RALV (Relationships Among Latent Variables) – ein Ansatz, der besonderes Augenmerk auf die Vermeidung von Verzerrungen der geschätzten Koeffizienten aufgrund von Multikollinearität legt.

Sowohl die Kovarianzstrukturanalyse als auch PLS weisen Einschränkungen bei der Berücksichtigung formativer Messmodelle auf. Die Kovarianzstrukturanalyse kann formative Messmodelle nur für exogene Variable valide abbilden, während dies in PLS für exogene und endogene Variablen möglich ist. Allerdings gehen formative Messmodelle in PLS grundsätzlich davon aus, dass die latente Variable durch die beobachteten Indikatoren vollständig bestimmt ist. Dagegen kann in der Kovarianzstrukturanalyse durch eine Residualgröße berücksichtigt werden, dass die Bedeutung der latenten Variable über die erhobenen Indikatoren hinausgeht.

Insbesondere bei kleineren Stichproben zeigt sich ein Nachteil der Kovarianzstrukturanalyse. Sie liefert oft kein brauchbares Ergebnis. Entweder ist die Lösung unzulässig, zum Beispiel aufgrund geschätzter negativer Varianzen, oder man erhält gar keine Lösung, weil das iterative Verfahren zur Berechnung der Koeffizienten nicht konvergiert. Nur durch zusätzliche Restriktionen, beispielsweise durch das Fixieren eines Pfadkoeffizienten auf einen bestimmten Wert, oder das Weglassen von Variablen, ergibt sich dann möglicherweise ein zulässiges Ergebnis. In PLS und verwandten Ansätzen treten diese Probleme nicht auf.

Indirekte und totale Effekte

Typisch für Strukturgleichungsmodelle sind indirekte Beziehungen zwischen latenten Variablen. In dem gezeigten Modell bestimmt LV₁ die Variable LV₄ sowohl direkt als auch indirekt über LV₃. Ergeben sich beispielsweise die in der Abbildung dargestellten Pfadkoeffizienten, so ist die Stärke des indirekten Effekts gleich dem Produkt der beiden Koeffizienten 0,4 × 0,3 = 0,12. Zusammen mit dem direkten Effekt von 0,2 beträgt der totale Effekt somit 0,2 + 0,12 = 0,32. Auch wenn der direkte Effekt kleiner ist, besitzt LV₁ insofern einen stärkeren Einfluss auf LV₄ als LV₂.

Beitrag aus planung&analyse 13/3 in der Rubrik „Statistik kompakt“

Autoreninformation

Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.

Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.

Literatur

Homburg, C; Pflesser, C.; Klarmann, M.: Strukturgleichungsmodelle mit latenten Variablen: Kausalanalyse. In: Hermann, A.; Homburg, C.; Klarmann, M. (Hrsg.): Handbuch Marktforschung, 3. Auflage, Wiesbaden, 2008, S. 547-577.

Lüken, J.; Schimmelpfennig, H.: Erfolgswirkung von Marken-Touchpoints. Neue Wege der Strukturgleichungsmodellierung für Treiberanalysen. In: planung & analyse, Jg. 38/2011, Nr. 4, S. 61-64.

Scholderer, J.; Balderjahn; I.: Was unterscheidet harte und weiche Strukturgleichungsmodelle nun wirklich? Ein Klärungsversuch zur LISREL-PLS-Frage. In: Marketing ZFP, Jg. 28/2006, Nr. 1, S. 57-70.

Zurück zur Übersicht

Share