Diskriminanzanalyse

Johannes Lüken / Dr. Heiko Schimmelpfennig

Ausgehend von einer Gruppierung von Objekten beschäftigt sich eine Diskriminanzanalyse mit der

1. Identifikation der Variablen bezüglich derer sich diese Gruppen voneinander trennen lassen
2. Zuordnung von „neuen“ Objekten zu den Gruppen auf Basis ihrer Variablenausprägungen (Klassifizieren)

Mit der ersten Aufgabe befasst sich dieser Beitrag, mit der zweiten der kommende Beitrag dieser Reihe.

 

Ableitung der Diskriminanzfunktionen

Abbildung 1 zeigt 12 Objekte, die anhand von zwei Eigenschaften charakterisiert und jeweils einer Gruppe (rot, blau und grün) zugeordnet sind. Mit Hineinlegen einer ersten Geraden gelingt es, die blaue und die grüne Gruppe vollständig voneinander zu trennen. Eine zweite Gerade trennt zudem eindeutig zwischen der blauen und der roten Gruppe.

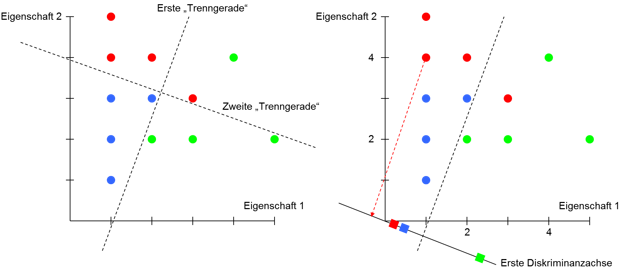Abbildung 1: Bestimmung einer Diskriminanzachse

Das Hineinlegen von Geraden in das durch die Eigenschaften aufgespannte Koordinatensystem korrespondiert mit der Bestimmung von Diskriminanzfunktionen, im Fall mit zwei Eigenschaften also von

y = b₀ + b₁×x₁ + b₂×x₂

wobei x₁ und x₂ die Eigenschaftsausprägungen, b₀ das Absolutglied sowie b₁ und b₂ die Diskriminanzkoeffizienten darstellen, in denen sich die diskriminatorische Bedeutung der Variablen widerspiegelt. Für die erste Trennung zwischen blau und grün ist insbesondere Eigenschaft 1 verantwortlich. Das heißt für die entsprechende Diskriminanzfunktion sollte der Betrag von b₁ größer als der von b₂ sein. Für die zweite Trennung zwischen blau und rot ist vor allem Eigenschaft 2 maßgeblich. Insofern sollte in einer zweiten Diskriminanzfunktion der Betrag von b₂ größer als der von b₁ sein. Durch Einsetzen der Eigenschaftsausprägungen in eine Diskriminanzfunktion lässt sich für jedes Objekt sein Diskriminanzwert y berechnen.

Ein Umstellen der Diskriminanzfunktion nach x₂ führt zu

x₂ = (y – b₀)/b₂ – b₁/b₂∙x₁

und beschreibt allgemein eine mögliche Trenngerade. Die Gerade, die durch den Ursprung des Koordinatensystems und orthogonal zu der nach x₂ umgestellten Diskriminanzfunktion verläuft, ist die Diskriminanzachse

x₂ = b₂/b₁×x₁.

Auf dieser können die Diskriminanzwerte dargestellt werden, indem von jedem Objekt das Lot auf die Diskriminanzachse gefällt wird, in der Abbildung beispielhaft dargestellt für ein Objekt der roten Gruppe. Ziel ist es, die Steigung b₂/b₁ der Diskriminanzachse so zu bestimmen, dass sich das arithmetische Mittel der Diskriminanzwerte einer Gruppe möglichst stark von denen der anderen Gruppen unterscheidet – wie in der Abbildung das der grünen ■ von dem der roten ■ und blauen ■. Die eingezeichnete erste Diskriminanzachse erfüllt dieses Ziel. Ihre Steigung determiniert das Verhältnis der Koeffizienten der ersten Diskriminanzfunktion, aber nicht deren absolute Höhe. Mathematisch sind die Koeffizienten so zu bestimmen, dass die Streuung der Diskriminanzwerte zwischen den Gruppen – die durch eine Diskriminanzfunktion erklärte Streuung – in Relation zur nicht erklärten Streuung der Diskriminanzwerte innerhalb der Gruppen möglichst groß wird. Um eindeutige Koeffizienten zu erhalten, werden diese schließlich so normiert, dass unter anderem der Mittelwert aller Diskriminanzwerte einer Diskriminanzfunktion gleich null ist. Somit ergeben sich für das Datenbeispiel die Diskriminanzfunktionen:

y₁ = -1,07 + 0,96×x₁ – 0,35×x₂             und           y₂ = -3,76 + 0,36×x₁ + 1,02×x₂

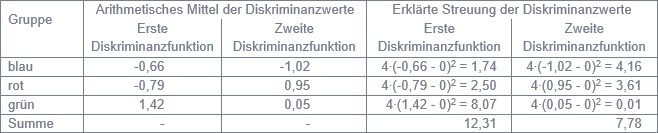
Abbildung 2: Berechnung der durch die Diskriminanzfunktionen erklärten Streuung

Die relative Wichtigkeit einer Diskriminanzfunktion für die Trennung zwischen den Gruppen wird durch den Anteil der durch sie erklärten Streuung an der gesamten erklärten Streuung gemessen (siehe Abbildung 2). Insofern besitzt die erste Diskriminanzfunktion eine relative Wichtigkeit von 61% und die zweite von 39%.

(Diskriminatorische) Bedeutung der Variablen

In den Diskriminanzkoeffizienten spiegeln sich nicht nur die diskriminatorische Bedeutung, sondern auch unterschiedliche Skalen wider. Um Vergleichbarkeit zu gewährleisten, sind die Koeffizienten zu standardisieren. Dazu werden sie multipliziert mit der Standardabweichung der entsprechenden Variable innerhalb der Gruppen. Diese beträgt für die erste Eigenschaft 0,97 und für die zweite 0,93. Somit ist beispielsweise der standardisierte Koeffizient für x₁ in der ersten Diskriminanzfunktion 0,96×0,97 = 0.93.

Zur Beurteilung der diskriminatorischen Bedeutung der Variablen werden alle Diskriminanzfunktionen herangezogen, um einen mittlereren Diskriminanzkoeffizienten zu berechnen. Dieser ist gleich dem mit der relativen Wichtigkeit der Diskriminanzfunktionen gewichteten Mittelwert des Betrags der standardisierten Diskriminanzkoeffizienten:

Für Eigenschaft 1: 0,61×0,93 + 0,39×0,34 = 0,70

Für Eigenschaft 2: 0,61×0,33 + 0,39×0,95 = 0,57

Insofern trennt in diesem Datenbeispiel Eigenschaft 1 zwischen den drei Gruppen etwas stärker als Eigenschaft 2.

 

Beitrag aus planung&analyse 15/6 in der Rubrik „Statistik kompakt“

 

Autoreninformation

Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.

Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.

 

Literatur

Backhaus, K.; Erichson, B.; Plinke, W.; Weiber, R.: Diskriminanzanalyse. In: Multivariate Analysemethoden, 13. Auflage, Berlin, 2011, S. 187-248.

Decker, R.; Temme, T.: Diskriminanzanalyse. In: Herrmann, A.; Homburg, C.: Marktforschung, 2. Auflage, Wiesbaden, 2000, S. 295-336.

 
<

---

Share