Entscheidungsbäume
Johannes Lüken / Dr. Heiko Schimmelpfennig
Allgemein stellen Entscheidungsbäume den Weg zu einer Entscheidung grafisch dar. In der Marktforschung werden sie eingesetzt, um Segmente zu bilden und Klassifikationsregeln zu bestimmen.
Ziele
Im Gegensatz zu der zumeist zur Segmentierung genutzten Clusteranalyse differenzieren Entscheidungsbäume zwischen einer abhängigen Variable und unabhängigen Variablen. Ziel ist es, Segmente in einer Stichprobe zu finden, die durch die unabhängigen Variablen definiert und hinsichtlich der abhängigen Variable möglichst homogen sind.
Somit helfen Entscheidungsbäume zu verstehen, wie die abhängige Variable und die unabhängigen Variablen zusammenhängen. Sie ermöglichen es, Regeln für die Klassifikation von Personen zu formulieren. Der Modalwert einer kategorialen abhängigen Variable beziehungsweise der Mittelwert einer metrischen abhängigen Variable eines Segments ist sodann eine Prognose eben dieser Variable auch für „neue“ Personen, die diesem Segment zugeordnet werden.
Beispiel
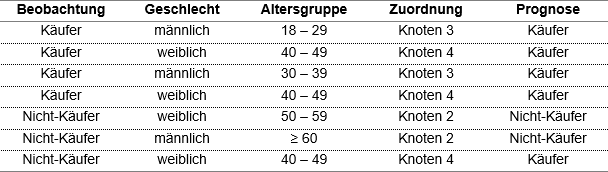
Auch wenn Entscheidungsbäume für größere Stichproben prädestiniert sind, lassen sie sich ebenso gut anhand eines kleinen Datenbeispiels veranschaulichen. Von sieben Personen sei neben dem Geschlecht und dem Alter bekannt, ob sie Käufer oder Nicht-Käufer eines Produkts sind (siehe Abbildung 1).
Abbildung 1: Datenbeispiel
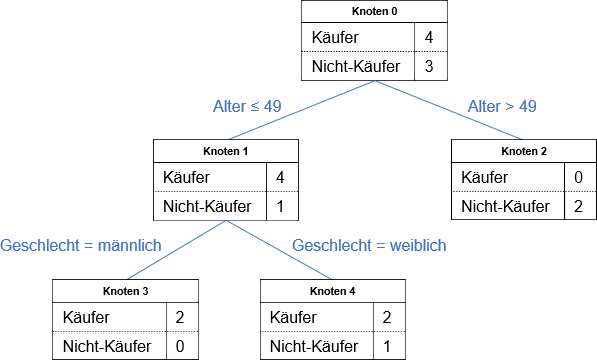
Abbildung 2: Entscheidungsbaum zum Datenbeispiel
In der Stichprobe befinden sich vier Käufer und drei Nicht-Käufer. Ziel ist es, diese so aufzuteilen, dass sich in den Segmenten entweder möglichst viele Käufer oder möglichst viele Nicht-Käufer befinden. In einem ersten Schritt kann anhand des Alters eine Teilgruppe identifiziert werden, die nur Nicht-Käufer enthält (Knoten 2). Damit ergibt sich eine erste Klassifikationsregel respektive Definition eines Segments:
Wenn älter als 49, dann Segment/Knoten 2 (Modalwert: Nicht-Käufer)
Die andere Teilgruppe (Knoten 1) wird in eimem zweiten Schritt anhand des Geschlechts aufgeteilt in ein Segment, dem nur Käufer angehören (Knoten 3), und ein Segment (Knoten 4), das zwei Käufer und einen Nicht-Käufer umfasst. Da alle drei weiblich sind und zu der Altersgruppe 40 – 49 Jahre zählen, kann dieses nicht weiter aufgeteilt werden. Daraus folgen zwei weitere Klassifikationsregeln:
Wenn jünger als 50 und männlich, dann Segment/Knoten 3 (Modalwert: Käufer)
Wenn jünger als 50 und weiblich, dann Segment/Knoten 4 (Modalwert: Käufer)
Abbildung 2 stellt den entsprechenden Entscheidungsbaum dar. Mit Hilfe der Klassifikationsregeln ergibt sich für die Stichprobe eine Trefferquote von 6/7.
Grundgedanke der Algorithmen zur Induktion von Entscheidungsbäumen ist das beispielhaft beschriebene rekursive Zerlegen eines vorliegenden Datensatzes. Jede Aufteilung erfolgt anhand einer unabhängigen Variable. Für die Auswahl dieser Variable und die genaue Aufteilung spielt die abhängige Variable eine entscheidende Rolle.
Gängige Algorithmen sind
- CHAID (Chi-Squared Automatic Interaction Detector)
- CART (Classification and Regression Tree)
- CTree (Conditional Inference Tree)
Prinzipiell können die Variablen beliebige Skalenniveaus aufweisen. Da die Algorithmen damit unterschiedlich umgehen sowie verschiedene Kriterien für die jeweilige Auswahl der Trennungsvariable anlegen, gibt es zu einem Datensatz mehrere mögliche Entscheidungsbäume. Diese können beispielsweise hinsichtlich der Trefferquote miteinander verglichen werden.
Beitrag aus planung&analyse 17/5 in der Rubrik „Statistik kompakt“.
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Rokach, L., Maimon, O.Z.: Data Mining with Decision Trees: Theory and Applications, 2. Auflage, Hackensack, 2015.
<