Signifikanz und Stichprobenumfang
Johannes Lüken / Dr. Heiko Schimmelpfennig
Bei der Tabellierung von Marktforschungsdaten ist es gang und gäbe, signifikante Unterschiede zwischen betrachteten Teilgruppen zu kennzeichnen. Nicht selten kommt es vor, dass eine Differenz zwischen zwei Gruppen als signifikant und eine größere Differenz zwischen zwei anderen Gruppen nicht als signifikant ausgewiesen wird. Eine mögliche Erklärung dafür ist, dass die ersten beiden Gruppen stärker besetzt sind als die anderen beiden.
Signifikanztest
Ein in einer Stichprobe beobachteter Effekt, zum Beispiel der Unterschied zwischen zwei Gruppen, ist signifikant, wenn dieser wahrscheinlich nicht zufällig aufgetreten ist. Man kann dann davon ausgehen, dass ein Unterschied auch in der entsprechenden Grundgesamtheit besteht. Die Prüfung auf Signifikanz erfolgt mit einem statistischen Test. Diesem liegt die Hypothese zugrunde, dass kein Effekt vorliegt. Auf Basis der Stichprobe wird die Wahrscheinlichkeit p bestimmt, mit dem Verwerfen der Hypothese einen Fehler zu begehen. Ist p kleiner als ein vorgegebenes Signifikanzniveau a (zumeist ist a = 0.05), so wird die Hypothese abgelehnt, das heißt der Effekt ist signifikant.
Abhängigkeit der Signifikanz vom Stichprobenumfang
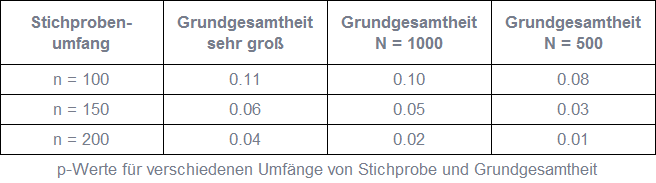
Es soll überprüft werden, ob sich das Ausprobieren eines Produkts positiv auf die Kaufbereitschaft auswirkt. Dazu wird die Kaufbereitschaft vor und nach dem Ausprobieren bei denselben zufällig ausgewählten Befragten auf einer sieben-stufigen Ratingskala erhoben. Im Mittel ergibt sich in der Stichprobe beispielsweise eine um 0.2 Skalenpunkte höhere Kaufbereitschaft nach dem Ausprobieren. Ist diese Erhöhung signifikant? Zur Beantwortung dieser Frage wird die einseitige Hypothese getestet, dass sich die Kaufbereitschaft nach dem Ausprobieren nicht erhöht. In der Tabelle sind die für mögliche Stichprobenumfänge und verschieden große Grundgesamtheiten resultierenden p-Werte dargestellt. Obwohl allen derselbe Mittelwert der Differenzen zwischen der Kaufbereitschaft vor und nach dem Ausprobieren sowie dieselbe Standardabweichung der Differenzen zugrunde liegt, unterscheiden sich die p-Werte. Im Fall einer sehr großen Grundgesamtheit ist die Verbesserung der durchschnittlichen Kaufbereitschaft für n = 100 und n = 150 nicht signifikant, da p größer als 0.05 ist. Für n = 200 ist sie dagegen signifikant.
Das heißt bei einem größeren Stichprobenumfang ist es wahrscheinlicher, dass die Hypothese abgelehnt wird und ein Effekt signifikant ist, als bei einem geringeren Stichprobenumfang. Insofern spricht das Verwerfen einer Hypothese bei einer kleinen Stichprobe für einen stärkeren Effekt in der Grundgesamtheit als bei einer großen Stichprobe.
Statistischer Hintergrund
Ob ein Effekt signifikant ist, hängt vom Ergebnis in der Stichprobe ebenso ab wie von der Stichprobenverteilung. Die Stichprobenverteilung beschreibt die Verteilung beispielsweise des Mittelwerts für alle denkbaren Stichproben eines bestimmten Umfangs. Die Abbildung zeigt die Stichprobenverteilungen für zwei unterschiedliche Stichprobenumfänge. Bei einem großen Stichprobenumfang ist die Verteilung viel schmaler, das heißt die Standardabweichung des Mittelwerts – der Standardfehler – kleiner. Die hellblaue Fläche unter der Kurve entspricht dem p-Wert beim großen Stichprobenumfang. Beim kleinen Stichprobenumfang ist der p-Wert trotz des gleichen Ergebnisses in der Stichprobe aufgrund des höheren Standardfehlers um die graue Fläche größer.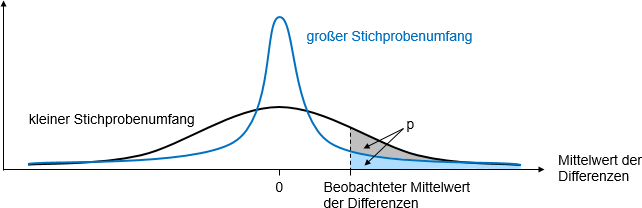
Konsequenz für gewichtete Daten
Eine Fallgewichtung verändert nicht nur das Ergebnis in der Stichprobe wie beispielsweise den Mittelwert. Der gewichtete Stichprobenumfang besitzt ebenfalls Einfluss auf den Ausgang des Signifikanztests. Um die Signifikanz eines Effekts nicht ungerechtfertigt zu begünstigen, sollte unbedingt vermieden werden, dass die Summe der Gewichte größer als der ursprüngliche Stichprobenumfang ist. Um die aufgrund der Gewichtung erhöhte Unsicherheit bei der Schätzung des Mittelwerts zu berücksichtigen, wird vielmehr empfohlen, einen reduzierten Stichprobenumfang – die so genannte „effective base“ – anzusetzen, die umso kleiner ist, je höher die Varianz der Fallgewichtungen ist.
Kleine Grundgesamtheiten und Vollerhebungen
Ist die Grundgesamtheit eher klein wie häufig bei B2B-Befragungen, wird mit der Stichprobe bereits ein großer Teil der Grundgesamtheit abgedeckt. Je höher das Verhältnis von Stichprobenumfang zur Größe der Grundgesamtheit ist, desto kleiner ist der Standardfehler. Das heißt auch aus diesem Grund wird die Stichprobenverteilung schmalgipfliger und der p-Wert damit kleiner. Der Vergleich der p-Werte in der Tabelle für einen bestimmten Stichprobenumfang und unterschiedlich große Grundgesamtheiten veranschaulicht diesen Zusammenhang.
Auf Basis einer Vollerhebung lassen sich die wahren Werte bestimmen. Das Formulieren von Hypothesen über die Werte in der Grundgesamtheit und Signifikanztests erübrigen sich dann. In dem Beispiel würde jede noch so kleine positive Abweichung des Mittelwerts von null einen positiven Effekt des Ausprobierens auf die Kaufbereitschaft bedeuten. Sinnvoll sind Signifikanztests dann nur, um zu überprüfen, ob ein beobachteter Effekt aufgrund von Messfehlern zustande gekommen ist.
Beitrag aus planung&analyse 12/6 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Behnke, J.: Lassen sich Signifikanztests auf Vollerhebungen anwenden? Einige essayistische Anmerkungen. In: Politische Vierteljahresschrift, Jg. 46/2005, Heft 1, S. O-1-O-15.
Kish, L.: Survey Sampling, New York et al., 1965, S. 427.
Lipovetzky, S.: Post-Stratification with Optimized Effective Base. In: Proceedings of the Survey Research Methods Section, American Statistical Association, 2007, S. 2313-2320.
<