Shapley Value

Johannes Lüken / Dr. Heiko Schimmelpfennig

Der Shapley Value ist ein Lösungskonzept der kooperativen Spieltheorie. Die ihm zugrunde liegende Berechnungsvorschrift findet darüber hinaus für Treiberanalysen sowie Produktlinien- oder Sortimentsoptimierungen Anwendung.

Der Shapley Value in der Spieltheorie

Die kooperative Spieltheorie untersucht, wie die Teilnehmer an einem Spiel durch die Bildung von Koalitionen ihren eigenen Nutzen maximieren können. Ein Beispiel: Drei Einzelhändlern – den Spielern 1, 2 und 3 – ist es möglich, durch Zusammenschlüsse zu Einkaufsgemeinschaften infolge günstigerer Einkaufspreise ihre Kosten zu reduzieren. Abbildung 1 gibt beispielhaft Gewinne (in Tausend Euro) an, die die Einzelhändler alleine beziehungsweise in den möglichen Koalitionen zusammen erzielen können.

Abbildung 1: Beispielhafte Gewinne von drei Spielern

Ziel ist, eine Koalition und eine Aufteilung des Gewinns dieser Koalition zu finden, bei denen es sich für keinen Spieler lohnt, eine andere Koalition einzugehen. Der Shapley Value liefert dafür eine Lösung. Dieser hängt von den Beiträgen eines Spielers zu allen möglichen Koalitionen ab. Der Beitrag eines Spielers besteht in der Steigerung des Gewinns, den er durch seinen Beitritt zu einer Koalition hervorruft.

Zur Berechnung des Shapley Value für einen Spieler werden alle Teilmengen der Menge aller Spieler betrachtet, die diesen Spieler enthalten. Für jede dieser Teilmengen wird vom Gewinn (allgemein: dem Wert der Koalition) mit ihm der Gewinn ohne ihn subtrahiert. Diese Differenz wird mit dem Faktor (k-1)!×(n-k)!/n! multipliziert, wobei n die Anzahl aller Spieler, k die Anzahl der Spieler der betrachteten Teilmenge sowie n! = n×(n-1)×(n-2)× ××× ×1 und 0! = 1 sind. Schließlich sind die gewichteten Differenzen über alle Teilmengen zu addieren.

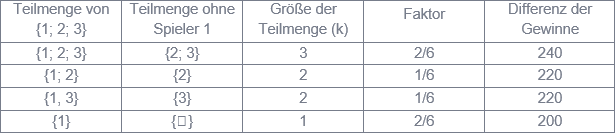Abbildung 2: Schema zur Berechnung des Shapley Value

Abbildung 2 veranschaulicht die Berechnung des Shapley Value SV₁ für den Spieler 1 im dargestellten Beispiel mit n = 3 Spielern. Dieser ist SV₁ = 2/6∙240 + 1/6∙220 + 1/6∙220 + 2/6∙200 = 220. Analog ergeben sich SV₂ = 140 und SV₃ = 240. Die Summe der drei Shapley Values ist gleich 600 und damit gleich dem Gewinn der „großen Koalition“ {1; 2; 3}. Abbildung 3 verdeutlicht, dass sich Spieler 1 weder in einer Koalition nur mit Spieler 2 oder nur mit Spieler 3 (in der die Verteilung ebenfalls nach dem Konzept des Shapley Value erfolgt) noch alleine besser stellt. Gleiches gilt für die Spieler 2 und 3, so dass {1; 2; 3} die gesuchte Koalition ist.

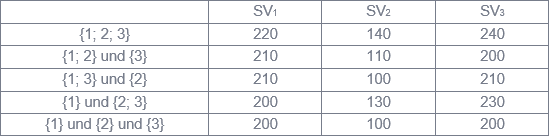Abbildung 3: Shapley Values für die Gewinne aus Abbildung 1

Treiberanalyse mittels Shapley Value Regression

Die Bestimmung der Bedeutung von Treibern einer abhängigen Variable wie beispielsweise der Kundenzufriedenheit ist grundsätzlich mit der multiplen linearen Regressionsanalyse möglich. Die standardisierten Regressionskoeffizienten messen die Einflussstärke der Treiber. Aufgrund der gewöhnlich hohen Interkorrelationen zwischen den Treibern ergeben sich jedoch häufig negative Regressionskoeffizienten, während die Korrelation zwischen dem Treiber und der abhängigen Variable positiv ist. Nicht nur dass sich die Zusammenhänge damit widersprechen, auch der Beitrag dieser Treiber ist dann negativ. Die Shapley Value Regression ist eine Möglichkeit, diese Problematik zu begegnen.

Die Berechnung des Shapley Value eines Treibers erfolgt analog zum dargestellten Beispiel zur Spieltheorie. Die Treiber sind die Spieler, das Bestimmtheitsmaß der linearen Regression einer Teilmenge mit k Treibern aller n betrachteten Treiber ist deren Wert. Der Shapley Value eines Treibers ist gleich der durchschnittlichen gewichteten Differenz zwischen dem Bestimmtheitsmaß aller Teilmengen mit dem Treiber und ohne diesen Treiber. Die Shapley Values aller Treiber spiegeln dann deren Bedeutung für die abhängige Variable wider. Sie sind immer alle positiv und stellen eine Aufteilung des Bestimmtheitsmaßes dar, das eine lineare Regression mit allen n Treibern aufweist.

Ergänzung einer TURF-Analyse um Shapley Values

Im Vordergrund der TURF-Analyse (Total Unduplicated Reach and Frequency) steht die Bestimmung der Nettoreichweite, das heißt der Anteil der Befragten in einer Stichprobe, die beispielsweise zumindest eine Variante einer Produktlinie kaufen würden. Die Nettoreichweite ermöglicht zum einen die Bestimmung des optimalen Umfangs der Produktlinie. Dieser ist erreicht, wenn die Nettoreichweite mit der Erweiterung der Produktlinie nicht mehr signifikant ansteigt. Zum anderen ist damit die Kombination der Varianten bestimmt, die für diesen Umfang die Nettoreichweite maximiert. Häufig ergeben sich jedoch mehrere Kombinationen, die die gleiche oder zumindest annähernd die optimale Nettoreichweite erzielen. Dann kann der Shapley Value ergänzend herangezogen werden. Die möglichen n Produktvarianten sind die Spieler, die Nettoreichweite einer Produktlinie mit k Varianten ist deren Wert. Der Shapley Value einer Variante entspricht dann ihrem durchschnittlichen gewichteten Beitrag zur Nettoreichweite aller Produktlinien mit dieser Variante.

Beispielsweise könnten sich bei fünf zur Auswahl stehenden Varianten A, B, C, D und E ein optimaler Umfang von drei und eine Rangordnung der Shapley Values von SV_D > SV_A > SV_B > SV_C > SV_E ergeben. Auch wenn die Nettoreichweite einer Produktlinie {A; C; D} dann größer wäre als die von {A; B; D} wird empfohlen, dass sich die Produktlinie aus den drei Varianten mit den höchsten Shapley Values zusammensetzt. Die Nettoreichweite wird nur für einen bestimmten Umfang ermittelt und geht davon aus, dass eine Produktlinie stets in vollem Umfang verfügbar ist. Der Shapley Value berücksichtigt dagegen alle Umfänge der Produktlinie, das heißt auch Situationen, in denen nicht alle Varianten vorrätig sind.

Beitrag aus planung&analyse 14/6 in der Rubrik „Statistik kompakt“

Autoreninformation

Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.

Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.

Literatur

Conklin, M.; Lipovetsky, S.: A Winning Tool for CPG. In: Marketing Research, Jg. 11/1999, Nr. 4, S. 22-27.

Lipovetsky, S.; Conklin, M.: Analysis of Regression in Game Theory Approach. In: Applied Stochastic Models in Business and Industry, Jg. 17/2001, Nr. 4, S. 319-330.

Shapley, L.S.: A Value for n-Person Games. In: Kuhn, H.W.; Tucker, A.W. (Hrsg.): Contribution to the Theory of Games, Vol. 2, Princeton, 1953, S. 307-317.

Zurück zur Übersicht

Share