STRUKTURGLEICHUNGSMODELL ZUM HYPOTHESENTEST LATENTER VARIABLEN

In der Marktforschung dienen Strukturgleichungsmodelle der Überprüfung kausaler Zusammenhänge zwischen Merkmalen. Ziel einer solchen Kausalanalyse ist es, hypothetische Wirkzusammenhänge zu durchleuchten. Ähnlich wie bei der Regressionsanalyse wird die Frage überprüft, in welche Richtung und wie stark eine oder mehrere sogenannte exogene Variablen eine oder mehrere endogene Variablen beeinflussen.

BEOBACHTBARE VARIABLEN ALS INDIKATOREN FÜR NICHT BEOBACHTBARE LATENTE VARIABLE

Dabei geht man ähnlich wie bei der Faktorenanalyse davon aus, dass das eigentlich interessierende Merkmal möglicherweise gar nicht beobachtbar ist, sondern “latent” die Grundlage für das beobachtete Verhalten oder die Meinungs- oder Einstellungsäußerung des Befragten darstellt. Letztere dienen als Indikatoren für die Ausprägung der dahinterliegenden grundlegenden Merkmale.

Grundlage für diese Pfadanalyse ist zunächst eine Hypothese, die aussagt, welche Merkmale von welchen Variablen beeinflusst werden. Komplexe Zusammenhangstrukturen können so aufgestellt werden, wobei Merkmale gleichzeitig unabhängig (also beeinflussend) und durch andere beeinflusst sein können. Die Pfadanalyse überprüft diese Hypothese, indem sie den Grad der Einflüsse misst und den Informationsgrad einer solchen Modellierung ermittelt.

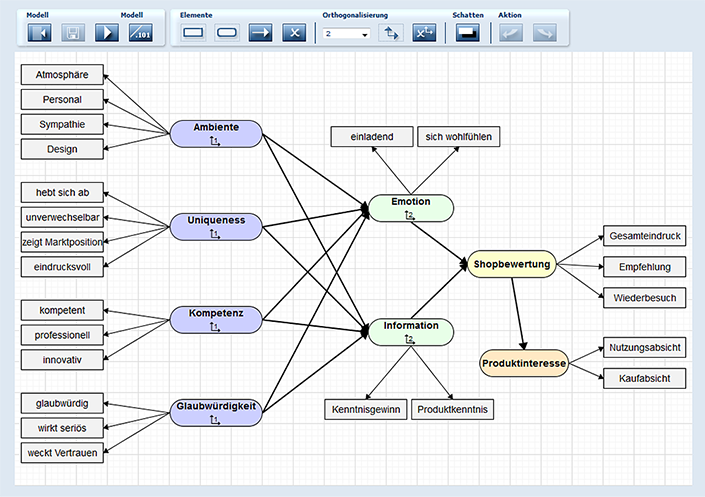
Strukturgleichungsmodell: Beispiel eines Kausalmodells – Erklärung einer Shopbewertung und des daraus resultierenden Produktinteresses

Die Pfadanalyse kann einen fehlerhaft angenommenen Richtungszusammenhang nicht erkennen. Die Richtung des Einflusses, also die Frage, ob Merkmal A Merkmal B beeinflusst oder umgekehrt, muss durch theoretische Vorüberlegungen geklärt werden.

Um die Koeffizienten inhaltlich sinnvoll interpretieren zu können, sollten die Einflussvariablen einer endogenen Variablen nach Möglichkeit unabhängig voneinander sein.

BAUEN SIE MIT DEM RALV-TOOL IHR EIGENES STRUKTURGLEICHUNGSMODELL AUF

Führen Sie mit dem ADABOX-Tool RALV (Relationships Among Latent Variables) Ihre eigenen stabilen und verzerrungsfreien Kausalanalysen (Strukturgleichungsmodelle) durch. RALV ermöglicht unter anderem das schnelle, sichere Durchspielen vieler Modellvarianten ohne lange Einarbeitung und spezielle Methodenkenntnis. Beinhaltet Orthogonalisierung als effektive Lösung zur Vermeidung von Verzerrungen geschätzter Pfadkoeffizienten aufgrund von Multikollinearität.