Praxisbeispiel: Faktorenanalyse

Ein Spirituosen-Hersteller plant, eines seiner Produkte, einen Kräuterlikör, im Umfeld der Wettbewerber optimal zu positionieren. Zu diesem Zweck soll eine Trackingstudie gezielte Veränderungen am Produkt über einen längeren Zeitraum begleiten. Um ein möglichst effizientes Messinstrument zu entwickeln, wurden aufgrund einer qualitativen Vorstufe Items definiert.

Im Rahmen eines Pretests bewerteten monadische Gruppen von ca. 200 Fällen das Kundenprodukt sowie 4 Wettbewerberprodukte anhand dieser Items. Ziel dieses Tests war es, die Validität der Items im Hinblick auf das Untersuchungsziel zu überprüfen.

Folgende Fragen sollten beantwortet werden:

• Lassen sich aufgrund der Items wesentliche Bewertungsdimensionen ableiten, die eine komprimierte Ergebnis-Darstellung ermöglichen?
• Sind alle Items ausreichend trennscharf, um diesen Dimensionen eindeutig zugeordnet werden zu können?
• Enthält die Liste Redundanzen, so dass durch Streichung von Items der Erhebungsaufwand reduziert werden kann?
• Enthalten die Items die intendierte Information (Prüfung der inhaltlichen Validität)?

Um die oben genannten Fragen zu beantworten, wurde eine Faktorenanalyse durchgeführt.

Folgende 16 Items wurden damit untersucht:

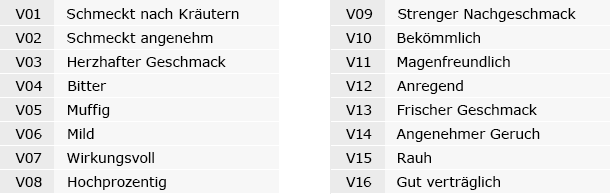
Die Bewertung erfolgte auf einer 7er -Skala, wobei  1 = „trifft überhaupt nicht zu“ und 7 = „trifft voll und ganz zu“ bedeuten.

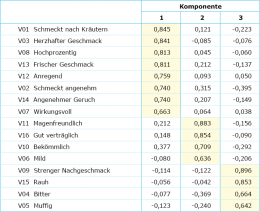
Die Faktorenanalyse lieferte folgende drei grundlegende Dimensionen:

Für diese Lösung sprachen sowohl technische als auch inhaltliche Aspekte.

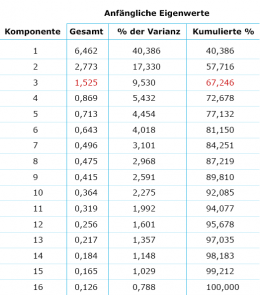
Eine Hauptkomponentenanalyse extrahiert Schritt für Schritt latente Merkmale (Hauptkomponenten), die einen maximalen Anteil der verbleibenden Varianz aufnehmen. Insgesamt lassen sich so viele latente Merkmale finden, wie beobachtete Merkmale (in diesem Fall 16) einfließen. Alle 16 Hauptkomponenten zusammen umfassen die gesamte Varianz der einfließenden 16 Items.  Im Gegensatz zu den beobachteten Merkmalen, die alle mit der Varianz von 1 einfließen, umfassen die Haupkomponenten von Schritt zu Schritt abnehmende Varianzanteile.

Abb. 1 zeigt die Eigenwerte der Hauptkomponenten, die bei diesem Verfahren der Varianz entsprechen. Deutlich ist der abnehmende Varianzanteil von der 1. bis zur 16. Hauptkomponente zu sehen. Die Summe aller 16 Eigenwerte beträgt wie die Varianz-Summe aller einfließenden Items 16 (=100%).

Um zu entscheiden, durch wie viele Dimensionen eine Liste von Eigenschaften im Wesentlichen repräsentiert wird, lassen sich folgende Kriterien heranziehen:

Eine verwendete Hauptkomponente soll mehr Information umfassen als ein einfließendes Item, also einen Eigenwert (Varianz) größer als 1 aufweisen.

Es lassen sich Grenzwerte für die durch die extrahierten Faktoren erfasste Varianz definieren. Als praktikable Richtgröße hat sich ein Anteil von zwei Dritteln erwiesen.

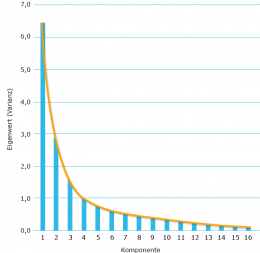
Ein „Knick“ im grafischen Verlauf der Eigenwerte (Scree Plot, siehe Abb. 2) deutet auf eine geeignete Anzahl von Faktoren hin. Extrahiert man weniger Dimensionen, verwirft man erhebliche Varianzanteile. Verwendet man mehr Dimensionen, dann steuern diese nur noch einen vergleichsweise unerheblichen Varianzanteil bei.

Die Ladungen (Korrelationen zwischen Items und Faktoren, Abb. 3) sollten eindeutige Zuordnungen erkennen lassen. D.h. die Absolutbeträge auf der Hauptdiagonalen (gelb hinterlegt) sollten hoch sein, die übrigen dagegen niedrig.

All diese Kriterien deuten sehr klar auf drei zugrunde liegende Dimensionen hin.

Neben diesen technischen Kriterien spricht auch die inhaltliche Betrachtung für die 3-Faktoren-Lösung:

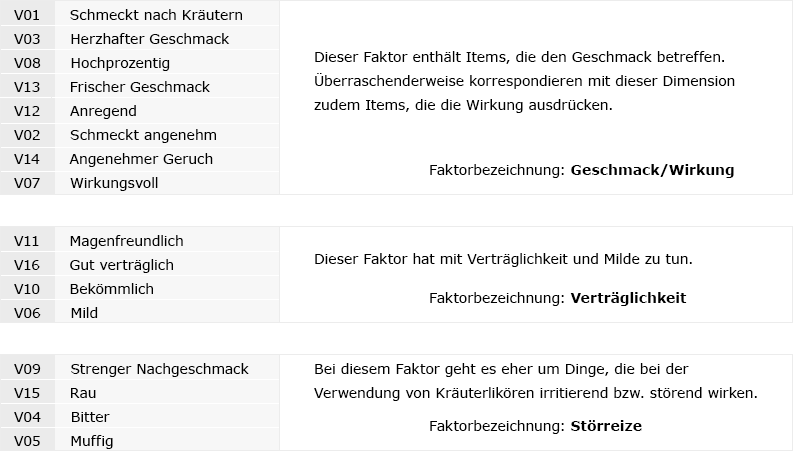
Dass auch „bitter“ zum Faktor 3 gehört zeigt, dass Konsumenten hiermit eher eine unangenehme Wahrnehmung verbinden. Ein weiterer Aspekt der inhaltlichen Validierung ist das überraschende Resultat, dass Geschmacks- und Wirkungsitems ähnlich wahrgenommen werden (Faktor 1). Die Tatsache, dass diese auch bei höheren Faktorlösungen „verbunden“ bleiben, zeigt, dass tatsächlich von einer gemeinsamen Grunddimension auszugehen ist.