
Random Forests und Boosted Trees
Johannes Lüken / Dr. Heiko Schimmelpfennig
Entscheidungsbäume dienen der Vorhersage einer zu beschreibenden (abhängigen) Variablen. Die (unabhängigen) Trennungsvariablen formen den Baum und können die Strukturen im analysierten Datensatz perfekt abbilden, das heißt die abhängige Variable genau „prognostizieren“. Für die Vorhersage der abhängigen Variablen in weiteren Daten kann ein solcher Baum aber dennoch ungeeignet sein. Ein möglicher Lösungsweg ist die Induktion mehrerer Bäume, von denen jeder einzelne auf einem etwas anderen Datensatz beruht. Random Forests und Boosted Trees sind zwei Methoden zur Erzeugung von Ensembles von Entscheidungsbäumen, deren zugrunde liegende Ideen anhand eines kleinen Beispiels mit einer dichotomen abhängigen Variable veranschaulicht werden.
Induktion eines Entscheidungsbaums
Trainingsdatensatz (siehe Abbildung 1 links) und Validierungsdatensatz (rechts) des Beispiels umfassen jeweils zehn Fälle, von denen fünf einer blauen und fünf einer orangenen Gruppe angehören. Für jeden Fall liegen zudem die Ausprägungen von zwei unabhängigen Variablen x1 und x2 vor. Abbildung 1 zeigt einen möglichen Entscheidungsbaum und die diesem Baum entsprechende Zerlegung des durch x1 und x2 aufgespannten Raums veranschaulicht durch die unterschiedlichen Hintergrundfarben. Zur besseren Nachvollziehbarkeit beschränkt sich der Baum auf Verzweigungen mit zwei Zweigen und Trennungen nur bei ganzen Zahlen. Die Fälle des Trainingsdatensatzes passen alle zur jeweiligen Hintergrundfarbe, das heißt der Baum ordnet jeden Fall der richtigen Gruppe zu. Nutzt man ihn zur Prognose des Validierungsdatensatzes, werden jedoch nur sechs Fälle richtig klassifiziert. Schneidet man die unterste Verzweigung weg, würde zwar ein Fall des Trainingsdatensatzes falsch zugeordnet, der Baum aber allgemeiner und somit nur zwei Fälle des Validierungsdatensatzes fehlklassifiziert.
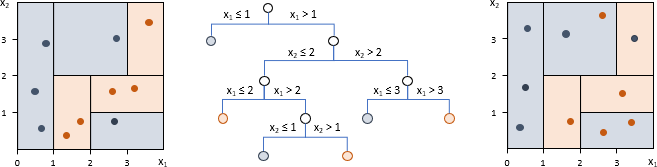
Abbildung 1: Vollständiger Entscheidungsbaum für den Trainingsdatensatz und Anwendung auf einen Validierungsdatensatz
Random Forests
Jeder Datensatz, für den ein Baum des Ensembles erzeugt wird, ist das Ergebnis einer zufälligen Auswahl aus dem Trainingsdatensatz mit Zurücklegen. Der Umfang dieser Stichprobe entspricht dem des ursprünglichen Datensatzes. In jedem Knoten erfolgt zudem eine zufällige Auswahl der infrage kommenden Trennungsvariablen. Abbildung 2a zeigt den ersten gezogenen Datensatz. Die größeren Kreise stehen für mehrfach gezogene Fälle. Als Trennungsvariable wurde zufällig x1 bestimmt. Die beste Trennung wird mit x1=3 erreicht: Nur ein Fall liegt in der falschen Gruppe. Allein der Übersichtlichkeit halber wird auf zusätzliche Aufteilungen bzw. Verzweigungen verzichtet. Die Abbildungen 2b und 2c zeigen zwei weitere gezogene Stichproben und die jeweils besten Aufteilungen. In beiden wurde x2 zufällig alsTrennungsvariable bestimmt. Diese drei Bäume (in echten Anwendungen sind es mehrere Hundert) werden zusammengefasst, indem jeder x1-x2-Kombination die Farbe (Gruppe) zugeordnet wird, mit der sie in den drei Bäumen am häufigsten vertreten ist. Abbildung 2d zeigt, dass damit acht Fälle des Validierungsdatensatzes korrekt klassifiziert werden.
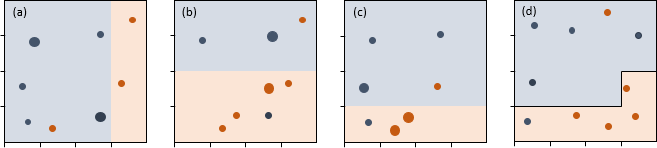
Abbildung 2: Ensemble von Bäumen mit Random Forests
Während bei Random Forests die einzelnen Bäume unabhängig voneinander sind, werden sie bei Boosted Trees so erzeugt, dass ein Baum die Fehler seines Vorgängers möglichst vermeidet. Zudem werden sie bewusst klein gehalten. Abbildung 3a veranschaulicht den ersten Baum, der nur aus einer Aufteilung besteht. Die beste Trennungsvariable ist x1. Zwei blaue Fälle werden aber der falschen Gruppe zugeordnet. Diese bekommen für die Induktion des zweiten Baums ein höheres Gewicht – gekennzeichnet durch die größeren Kreise in Abbildung 3b. Für diesen Datensatz bleibt x1 zwar die beste Trennungsvariable, aufgrund der Gewichtung verschiebt sich aber die Aufteilung. Nun werden drei orangene Fälle falsch zugeordnet. Vor der Erzeugung des nächsten Baumes erhalten diese ein höheres Gewicht etc. Erfolgt die Zusammenfassung der drei Bäume analog zu Random Forests, ergibt sich Abbildung 3d. Auch hiermit werden acht Fälle des Validierungsdatensatzes richtig klassifiziert.
Im Allgemeinen gelten Random Forests als die einfacher anzuwendende Methode, da Boosted Trees eine Reihe von Einstellungen erfordern, um ihre ganze Stärke ausspielen zu können.
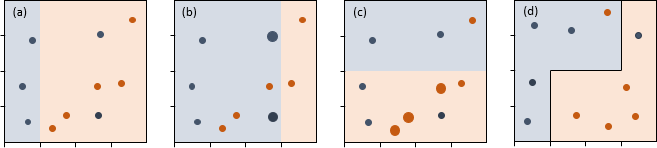
Abbildung 3: Ensemble von Bäumen mit Boosted Trees
Beitrag aus planung&analyse 18/3 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
James, G.; Witten, D.; Hastie, T.; Tibshirani, R.: Tree-Based Methods. In: An Introduction to Statistical Learning, New York, 2017, S. 303-335.
Ray, S.: Quick Introduction to Boosting Algorithms in Machine Learning, 2015, https://www.analyticsvidhya.com/
<






