Power eines statistischen Tests
Johannes Lüken / Dr. Heiko Schimmelpfennig
Ab und an ist man vielleicht verwundert, dass zum Beispiel ein Unterschied zwischen zwei Mittelwerten als nicht signifikant ausgewiesen wird. Ob dann davon ausgegangen werden soll, dass tatsächlich kein Unterschied besteht, ist abhängig von der Power des Tests bzw. der Teststärke. Das heißt es ist zu überprüfen, ob der Effekt eine „faire“ Chance hatte, auf Basis der Stichprobe erkannt zu werden.
Signifikanztest und Signifikanzniveau
Ein Signifikanztest beginnt mit dem Aufstellen der Hypothese, dass kein Effekt vorliegt. Diese lautet zum Beispiel, dass die Differenz der Mittelwerte eines Merkmals in zwei Gruppen gleich Null ist. Wäre diese Hypothese wahr und man würde sehr viele verschiedene Stichproben des gleichen Umfangs ziehen, so ergäben sich viele Stichproben mit einer Differenz der Mittelwerte nahe Null und nur vergleichsweise wenige mit einer Differenz, die deutlich von Null abweicht. Bei genügend großem Stichprobenumfang sind die Differenzen der Mittelwerte aller möglichen Stichproben annähernd normalverteilt.
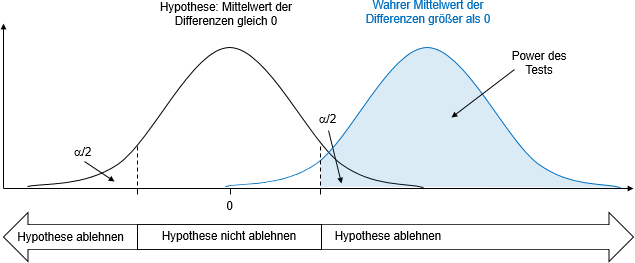
Tatsächlich wird aber nur eine Stichprobe gezogen. Anhand der Differenz für diese Stichprobe ist die Entscheidung zu treffen, ob die Hypothese abgelehnt wird oder nicht. Durch Vorgabe des Signifikanzniveaus wird der Bereich bestimmt, innerhalb dessen trotz einer beobachteten Differenz ungleich Null die Hypothese nicht abgelehnt wird. Außerhalb dieses Bereichs wird die Hypothese abgelehnt, obwohl sie eigentlich richtig ist. Allerdings weiß man dies nicht. Man geht vielmehr davon aus, dass die positive oder negative Abweichung von Null so groß ist, dass sie wohl nicht mehr zufällig zustande gekommen ist. Die Wahrscheinlichkeit eine Stichprobe zu ziehen, bei der die Hypothese fälschlicherweise abgelehnt wird – der Fehler 1. Art – entspricht dem vorgegebenen Signifikanzniveau a.
Power und Fehler 2. Art
Ist in der Grundgesamtheit die (wahre, aber unbekannte) Differenz der Mittelwerte ungleich Null, so verschiebt sich die tatsächliche Verteilung der Differenzen aller möglichen Stichproben im Vergleich zur hypothetischen Differenz von Null nach links oder wie in der Abbildung nach rechts. Der in der Tat vorhandene Unterschied wird dann identifiziert, wenn die Hypothese „Es liegt kein Effekt vor“ abgelehnt wird. Somit kennzeichnet in der Abbildung die hellblaue Fläche die Wahrscheinlichkeit, eine Stichprobe zu ziehen, mit der der Effekt erkannt wird. Diese Wahrscheinlichkeit ist die Teststärke oder die Power des Tests. Die (Gegen-)Wahrscheinlichkeit, einen vorliegenden Effekt nicht aufzudecken, wird als Fehler 2. Art bezeichnet.
Die Power dieses Tests ist bei vorgegebenem Signifikanzniveau abhängig von der wahren Differenz der Mittelwerte und von dem Standardfehler der Differenz. Eine größere Differenz führt im Beispiel der Abbildung zu einer Verschiebung der Normalverteilungskurve noch weiter nach rechts. Die Power des Tests steigt. Ein kleinerer Standardfehler, das heißt kleinere Standardabweichungen und/oder größere Umfänge der beiden Gruppen, macht die Verteilung schmalgipfliger. Auch damit steigt die Power des Tests.
Bestimmung der Power ex post
Häufig wird vorgeschlagen, dass bei einem Signifikanzniveau von 5% die Power des Tests mindestens 80% betragen sollte, damit bei einem nicht signifikanten Effekt davon ausgegangen werden kann, dass kein Effekt vorliegt. Anderenfalls wird empfohlen, ein nicht signifikantes Ergebnis nicht zu interpretieren. Zur Bestimmung der Teststärke müsste die wahre Stärke des Effekts bekannt sein. Dann hätte man aber gar keinen Test mehr durchführen müssen. Ein Ausweg ist, die Ergebnisse der Stichprobe als Schätzwerte heranzuziehen: Die Differenz der Mittelwerte und ihr Standardfehler in der Stichprobe bestimmen die Form der Normalverteilung der Differenzen der Mittelwerte. Damit kann die hellblaue Fläche unter der Normalverteilungskurve und somit die empirische Power des Tests im Nachhinein berechnet werden.
Abbildung: Stichprobenverteilungen für den hypothetischen und wahren Mittelwert der Differenzen
Beitrag aus planung&analyse 16/5 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Kähler, W.-M.: Statistische Datenanalyse, 5. Auflage, Wiesbaden, 2008.
Platz, F.; Kopiez, R.; Lehmann, M.: Statistische Poweranalyse als Weg zu einer ‚kraftvolleren‘ Musikpsychologie im 21. Jahrhundert. In: Auhagen, W.; Bullerjahn, C.; Höge, H. (Hrsg.): Populäre Musik, Göttingen, 2012, S. 165-179.
<