Nicht-lineare Regression
Johannes Lüken / Dr. Heiko Schimmelpfennig
Die lineare Regressionsanalyse geht davon aus, dass der Zusammenhang zwischen den unabhängigen und der abhängigen Variable linear ist. Diese Annahme ist zwar in vielen Fällen angebracht, mitunter ist aber der Einsatz der nicht-linearen Regression erforderlich, mit der auch andere Formen des Zusammenhangs untersucht werden können.
Beispiel aus der Sensorik
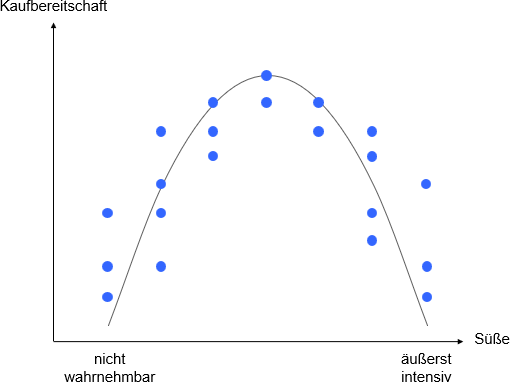
Es wird die Abhängigkeit der Kaufbereitschaft für eine Limonade von einer Eigenschaft wie der Süße betrachtet. Die Süße wird gemessen auf einer Skala von „nicht wahrnehmbar“ bis „äußerst intensiv“. Es ist zu vermuten, dass für die meisten Befragten eine Ausprägung zwischen den Extremen ideal ist, das heißt zu der höchsten Kaufbereitschaft führt. Geringe Abweichungen von der Idealausprägung beeinflussen die Kaufbereitschaft kaum, große Abweichungen sehr. Bei einem linearen Zusammenhang müsste die gleiche Veränderung der Süße immer zu derselben Veränderung der Kaufbereitschaft führen unabhängig von der Intensität der Süße. Das ist hier nicht der Fall. Der Zusammenhang zwischen Süße und Kaufbereitschaft kann vielmehr duch eine quadratische Funktion – eine nach unten geöffnete Parabel – gut beschrieben werden (siehe Abbildung 1).
Abbildung 1: Quadratischer Zusammenhang zwischen Süße und Kaufbereitschaft
Nicht-lineare Regression
Bezeichnen x die Süße und y die Kaufbereitschaft, so lautet die Regressionsfunktion
y = b0 + b1·x + b2·x2
Diese Regressionsfunktion ist wegen x2 nicht-linear in den Variablen. Ebenso wäre z.B. eine Regressionsfunktion mit Regressoren x-1 oder ex nicht-linear in den Variablen. Eine Regressionsfunktion ist nicht-linear in den Parametern, wenn sie Koeffizienten wie b-1 oder b2 enthält.
Die Koeffizienten einer nicht-linearen Regressionsfunktion können mit iterativen Verfahren geschätzt werden. Häufig ist eine Funktion jedoch linearisierbar. Dann lässt sich mit den gängigen Tools zur linearen Regressionsanalyse eine analytische Lösung finden. Die Linearisierung kann mittels Variablensubstitution bzw. -transformation möglich sein. In dem Beispiel einer quadratischen Regressionsfunktion wird durch x1 = x und x2 = x²
y = b0 + b1·x1+ b2·x2
zu einer Funktion, die linear in allen Parametern und Variablen ist. In der praktischen Umsetzung geht somit die Süße sowohl mit ihren Originalwerten für x1 als auch mit den quadrierten Werten für x2 in die Schätzung der Regressionskoeffizienten b0, b1 und b2 ein. Allgemein zeigt ein Vergleich des Bestimmtheitsmaßes einer nicht-linearen Regression mit dem der linearen Regression y = b0 + b1·x, ob von einem nicht-linearen statt linearen Zusammenhang ausgegangen werden sollte.

Bestimmung von Treibertypen mittels nicht-linearer Regression
Im Hinblick auf den Zusammenhang zwischen dem Leistungsniveau einer Eigenschaft und der Zufriedenheit mit einem Produkt oder einer Dienstleistung werden im Allgemeinen drei Treibertypen unterschieden:
- Basistreiber:
Es wird ein Mindestniveau erwartet. Wird dieses unterschritten, führt dies zu Unzufriedenheit. Wird es übertroffen, resultiert daraus aber keine Zufriedenheit. - Begeisterungstreiber:
An die Eigenschaft gibt es keine Erwartungen. Erreicht sie dennoch ein gutes Leistungsniveau, führt dies zu Zufriedenheit. Falls nicht, bleibt dies ohne Auswirkung. - Linearer Treiber:
Entsprechend dem Leistungsniveau können sowohl Zufriedenheit als auch Unzufriedenheit entstehen.
Die Kategorisierung der Treiber mit einer Kano-Analyse bedeutet hohen Erhebungsaufwand. Liegen die Zufriedenheit und die Beurteilung der Leistungsniveaus jedoch bereits vor, können die Treibertypen mittels Penalty- & Reward-Analyse, aber ebenso mithilfe der nicht-linearen Regression bestimmt werden.
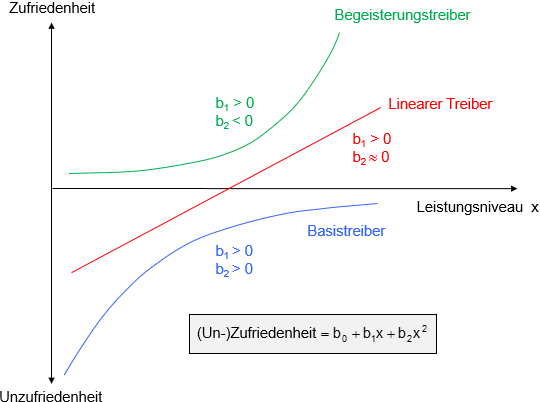
Abbildung 2: Darstellung der Treibertypen als lineare und quadratische Funktionen (Quelle: Schimmelpfennig (2016))
Dazu wird eine quadratische Regression der Gesamtzufriedenheit auf das Leistungsniveau einer Eigenschaft durchgeführt. Der Koeffizient b2 bestimmt dann den Treibertyp (siehe Abbildung 2). Ist b2 positiv, ist die Parabel nach unten geöffnet. Der linke Ast spiegelt somit die Definition eines Basistreibers wider. Ein Begeisterungstreiber wird durch den rechten Ast einer bei negativem b2 nach oben geöffneten Parabel repräsentiert. Ist b2 nahe Null, so liegt ein linearer Treiber vor.
Beitrag aus planung&analyse 19/4 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
von der Lippe, P.: Regressionsanalyse. In: Deskriptive Statistik, Stuttgart, Jena, 1993, S. 258-301.
Schimmelpfennig, H.: Bekannte, aktuelle und neue Anforderungen an Treiberanalysen. In: Keller, B. et al. (Hrsg.): Marktforschung der Zukunft – Mensch oder Maschine?, Wiesbaden, 2016, S. 231-243.
<