Mittelwertvergleiche mittels t-Test
Johannes Lüken / Dr. Heiko Schimmelpfennig
Der t-Test für unverbundene bzw. unabhängige Stichproben zählt zu den am häufigsten genutzten statistischen Tests. Er überprüft, ob sich die Mittelwerte metrischer Merkmale in zwei Test- oder Teilgruppen signifikant voneinander unterscheiden.
Einführungsbeispiel
Auf einer 7-stufigen Rating-Skala wurde die Kaufabsicht für ein neues Produkt erhoben. Die durchschnittliche Kaufabsicht beträgt in der (Teil-)Stichprobe der weiblichen Befragten 5, in der der männlichen Befragten 4. Ist der Unterschied signifikant? Auskunft darüber gibt der p-Wert als Ergebnis eines geeigneten statistischen Tests. Der t-Test für unverbundene Stichproben ist geeignet, da die Gruppen der männlichen und weiblichen Befragten sich nicht überschneiden. Er geht von der Hypothese aus, dass die Mittelwerte in den Grundgesamtheiten gleich sind. Der p-Wert gibt die Wahrscheinlichkeit an, mit dem Verwerfen dieser Hypothese einen Fehler zu begehen. Ist der p-Wert kleiner als ein vorgegebenes Signifikanzniveau a (zumeist ist a = 0,05), so wird die Hypothese gleicher Mittelwerte abgelehnt, weil die Wahrscheinlichkeit sehr gering ist, mit dieser Entscheidung falsch zu liegen. Der Unterschied wäre dann signifikant.
Konstruktion der Teststatistik
Jedem statistischen Test liegt eine Teststatistik zugrunde, deren Wert auf Basis der Stichprobe berechnet wird. Dieser wiederum determiniert den p-Wert. Für den Vergleich der Mittelwerte liegt es nahe, dass in die Teststatistik die Differenz der Mittelwerte eingeht. Trotz gleicher Differenzen können sich jedoch die p-Werte und somit auch die Beurteilungen im Hinblick auf die Signifikanz unterscheiden.
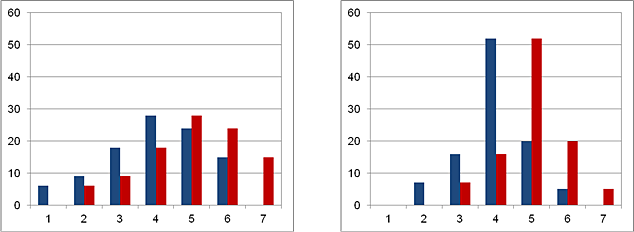
Abbildung: Häufigkeitsverteilungen der Antworten von jeweils zwei Teilgruppen
Die Abbildung zeigt die Häufigkeitsverteilungen der Antworten auf die Kaufabsicht in zwei Untersuchungen. In beiden ist der Mittelwert für die blaue Gruppe 4 und für die rote Gruppe 5. Allerdings ist die Streuung der Antworten der Untersuchung im linken Teil der Abbildung größer als im rechten. Die blaue und rote Gruppe scheinen sich im Fall mit geringerer Streuung deutlicher zu unterscheiden, da sich die beiden Verteilungen weniger überlappen. Daher wird die Differenz der Mittelwerte in Relation zur Standardabweichung s des Merkmals beurteilt.
Bei im Vergleich zur Grundgesamtheit großen Stichproben ist die Gefahr kleiner, dass die Mittelwerte der Stichproben sehr von den Mittelwerten der Grundgesamtheiten abweichen, als bei kleineren Stichproben. Um dies zu berücksichtigen, wird der Quotient aus Mittelwertdifferenz und Standardabweichung mit einem Faktor multipliziert, der die Teilstichprobenumfänge n1 und n2 beinhaltet:
Die gemeinsame Standardabweichung s ergibt sich aus den mit n1 und n2 gewichteten Standardabweichungen innerhalb der Teilstichproben. Die Teststatistik t folgt unter der Annahme der Gültigkeit der Hypothese gleicher Mittelwerte in den Grundgesamtheiten dann einer t- bzw. Student-Verteilung, die der Normalverteilung sehr ähnlich ist und dem Test seinen Namen gibt.
Eine vorliegende Stichprobe ist immer nur eine von sehr vielen desselben Umfangs, die sich bei einer Zufallsauswahl ebenso hätten ergeben können. Der p-Wert ist die Wahrscheinlichkeit, eine Stichprobe zu ziehen, für die der Wert der Teststatistik vom Betrag größer ist als der der tatsächlich gezogenen Stichprobe. Je höher der berechnete t-Wert ist, desto geringer ist die Wahrscheinlichkeit, dass der einer anderen Stichprobe größer ist. Das heißt ein Unterschied zwischen zwei Mittelwerten ist umso eher signifikant,
- je größer die Differenz der Mittelwerte ist,
- je kleiner die Standardabweichung in den beiden Gruppen ist und
- je größer die Umfänge der Teilstichproben sind.
Ob sich die Kaufabsicht zwischen den Geschlechtern signifikant unterscheidet, hängt demnach nicht nur von der beobachteten Differenz der Mittelwerte ab, sondern auch, wie viele befragt wurden, und wie heterogen die Antworten sind.
Voraussetzungen
Die Größe der beiden Gruppen sollte jeweils mindestens 30 betragen, wenn nicht von einer Normalverteilung des Merkmals in den Grundgesamtheiten ausgegangen werden kann. Anderenfalls ist ein Test aus der Gruppe der nicht-parametrischen (verteilungsfreien) Verfahren zu nutzen wie beispielsweise der Mann & Whitney U-Test.
Sind die Stichprobenumfänge unterschiedlich hoch, beeinträchtigt dies kaum die Testergebnisse solange die Varianzen in den Grundgesamtheiten als gleich gelten können. Sind Stichprobenumfänge und Varianzen in den beiden Gruppen verschieden, ist eine Variante des beschriebenen Tests, der Welch-Test, einzusetzen.
Beitrag aus planung&analyse 16/2 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Bortz, J.; Schuster, C.: Tests zur Überprüfung von Unterschiedshypothesen. In: Statistik für Human- und Sozialwissenschaftler, 7. Auflage, Berlin, 2010, S. 117-136.
Lüken, J.; Schimmelpfennig, H.: Einführung in Signifikanztests. In: planung & analyse, Jg. 39/2012, Nr. 5, S. 24.
<