Mehrfaktorielle Varianzanalyse
Johannes Lüken / Dr. Heiko Schimmelpfennig
Häufig interessiert der Einfluss, den zwei oder mehr Merkmale auf eine metrische Variable besitzen. Sind die unabhängigen Merkmale nominal skaliert, kann dazu die mehrfaktorielle Varianzanalyse eingesetzt werden. Um die ihr zugrunde liegende Idee darzustellen, genügt die Betrachtung der zweifaktoriellen Varianzanalyse.
Zweifaktorielle Varianzanalyse
Es soll herausgefunden werden, ob die Kaufbereitschaft für ein Produkt von der Verpackung abhängt, die sich in Form (quadratisch oder rund) und Farbe (rot, blau oder grün) unterscheidet. Zu allen 2 ∙ 3 = 6 Verpackungen, die durch die Kombinationen der Faktorstufen bestimmt sind, werden zufällig ausgewählte Personen nach ihrer Kaufbereitschaft gefragt.
Mit der einfaktoriellen Varianzanalyse kann „nur“ untersucht werden, ob sich die Mittelwerte der Kaufbereitschaft signifikant zwischen den sechs Gruppen der Befragten unterscheiden. Mit der zweifaktoriellen Varianzanalyse wird dagegen überprüft, ob Farbe und/oder Form der Verpackung die Kaufbereitschaft beeinflussen. Darüberhinaus kann ein Interaktionseffekt zwischen den beiden Faktoren bestehen, wenn sich der Einfluss der Form in Abhängigkeit der Farbe oder der Einfluss der Farbe in Abhängigkeit der Form ändert.
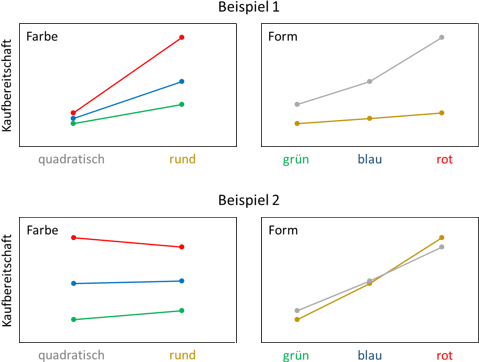
Zur grafischen Analyse der Einflüsse werden die Mittelwerte der Kaufbereitschaft für die sechs Gruppen in einem Profildiagramm abgetragen. Die Abbildung zeigt dies beispielhaft für zwei verschiedene Erhebungen. Um eine zweidimensionale Darstellung zu ermöglichen, wird entweder auf der horizontalen Achse nach der Form (in der Abbildung jeweils links) oder nach der Farbe (in der Abbildung jeweils rechts) differenziert. Zur Verdeutlichung können die Mittelwerte, die jeweils zu derselben Stufe des zweiten Faktors gehören, durch Linien miteinander verbunden werden.
Abbbildung: Beispielhafte Profildiagramme
Wenn sich in einem Diagramm mindestens zwei der Geraden nicht schneiden, deutet dies auf einen Einfluss des Faktors hin, der die unterschiedlichen Linien definiert. So ist in Beispiel 1 der Mittelwert der roten Verpackung sowohl bei der quadratischen als auch bei der runden Verpackung höher als die Mittelwerte bei der blauen beziehungsweise grünen Verpackung. Die Farbe besitzt einen Einfluss. Gleiches gilt in Beispiel 2.
In Beispiel 1 sind die Mittelwerte für eine quadratische Verpackung bei allen Farben höher als die bei der runden Verpackung. In Beispiel 2 sind sie dagegen mal höher und mal niedriger. Somit beeinflusst in Beispiel 1 die Form die Kaufbereitschaft, in Beispiel 2 nicht.
Zudem sind die Unterschiede in Beispiel 1 zwischen den drei Mittelwerten bei einer quadratischen Verpackung deutlich kleiner als die bei einer runden Verpackung. Das heißt, die Höhe des Einflusses der Farbe ist abhängig von der Form der Verpackung. Zwischen Farbe und Form besteht demnach ein Interaktionseffekt. In Beispiel 2 sind die Differenzen dagegen fast gleich, die Linien somit nahezu parallel. Zwischen Farbe und Form liegt hier kein Interaktionseffekt vor.
Signifikanztest und Effektstärke
Die Streuung der individuellen Kaufbereitschaften um die mittlere Kaufbereitschaft über alle Befragten wird erklärt durch die Form, die Farbe und die Interaktion von Form und Farbe. Die noch verbleibende Streuung kann nicht erklärt werden. Ist beispielsweise die auf die Form zurückzuführende Streuung deutlich größer als die nicht erklärte Streuung, spricht dies gegen die Hypothese, dass die Form keinen Einfluss auf die Kaufbereitschaft besitzt. Gleiches gilt für die Farbe wie auch für den Interaktionseffekt. Das vorgegebene Signifikanzniveau bestimmt, wie groß das Verhältnis mindestens sein muss, damit der Einfluss statistisch signifikant ist.
In der zwei- beziehungsweise mehrfaktoriellen Varianzanalyse wird die Effektstärke zur Beurteilung der Relevanz des Ergebnisses durch das partielle Eta² gemessen. Dies ist beispielsweise für die Form der Verpackung der Anteil der durch die Form erklärten Streuung an der Summe aus dieser Streuung und der nicht erklärten Streuung. Nach Cohen (1988) ist in der Varianzanalyse generell ein Effekt ab 0,01 klein, ab 0,06 mittel und ab 0,14 groß.
Beitrag aus planung&analyse 17/3 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Cohen, J.: Statistical Power Analysis for the Behavioral Sciences, 2. Auflage, Hillsdale, 1988.
Rasch, B.; Friese, M.; Hofmann, W.; Naumann, E.: Zweifaktorielle Varianzanalyse. In: Quantitative Methoden 2, 4. Auflage, Berlin, Heidelberg, 2014, S. 35-63.
<