Maximum-Likelihood-Schätzung

Johannes Lüken / Dr. Heiko Schimmelpfennig

Die Maximum-Likelihood (ML)-Methode zählt zu den gängigsten Verfahren zur Schätzung von Parametern einer Grundgesamtheit auf Basis einer Stichprobe. Ihr Grundgedanke ist, den Wert eines Parameters so zu bestimmen, dass das Auftreten der konkreten Beobachtungen in der Stichprobe am wahrscheinlichsten ist.

Maximum-Likelihood-Prinzip

Ein Anbieter möchte wissen, mit welcher Wahrscheinlichkeit ein Kunde infolge eines Mailings bei ihm kauft. Bezeichnet p diese Wahrscheinlichkeit, so ist 1-p die Wahrscheinlichkeit, dass kein Kauf erfolgt. Beispielsweise zeigen in einer Stichprobe fünf zufällig ausgewählte Kunden folgende Reaktionen:

Kauf – Kein Kauf – Kein Kauf – Kauf – Kein Kauf

Da die Kaufentscheidungen unabhängig voneinander sind, beträgt die Wahrscheinlichkeit, eine Stichprobe mit diesen Ergebnissen zu beobachten

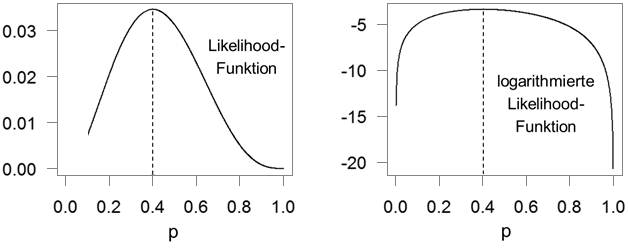
In der Abbildung ist die Likelihood-Funktion L dargestellt. Sie veranschaulicht für alle möglichen Werte des Parameters p in der Grundgesamtheit, wie wahrscheinlich dann die von den fünf Kunden gezeigten Reaktionen sind. Das ML-Prinzip geht nun davon aus, dass die Kaufentscheidungen in dieser Stichprobe zustande gekommen sind, weil die Wahrscheinlichkeit genau dafür am größten war. Insofern ist p so zu bestimmen, dass die Wahrscheinlichkeit für das Auftreten dieser Stichprobe – die Likelihood-Funktion – maximal wird. Zur analytischen Bestimmung des Maximums wird die erste Ableitung der Likelihood-Funktion gleich Null gesetzt und anschließend nach p aufgelöst. Es ergibt sich . Das heißt, die ML-Schätzung entspricht dem Anteil der Käufer in der Stichprobe (2 von 5).

Häufig wird die logarithmierte Likelihood-Funktion verwendet, da sie leichter zu maximieren ist. Zudem bewegen sich die resultierenden Werte eher in einem nachvollziehbaren Bereich, während die Werte der Likelihood-Funktion bei größeren Stichproben sehr klein werden können. Beide Funktionen erreichen ihr Maximum bei denselben Parameter-Werten (siehe Abbildung).

Abbildung: Likelihood-Funktion und logarithmierte Likelihood-Funktion

ML-Schätzung für Regressionsmodelle

Zumeist interessiert weniger die (für alle gleiche) Kaufwahrscheinlichkeit als vielmehr die Einflussgrößen der Kaufentscheidung. Um diese zu untersuchen, werden neben der Kaufentscheidung für jeden Kunden die Ausprägungen weiterer Variablen erfasst, zum Beispiel sozio-demografischer Merkmale wie Alter, Einkommen und Haushaltsgröße.

Die individuelle Kaufwahrscheinlichkeit eines Kunden ist dann abhängig von den Ausprägungen und den Regressionskoeffizienten der Variablen. In einem binären Logistischen Regressions- bzw. Logit-Modell ist diese individuelle Kaufwahrscheinlichkeit

mit zum Beispiel

Zur Maximierung der Likelihood-Funktion sind jetzt die Koeffizienten zu bestimmen. Dies ist analytisch jedoch nicht möglich. Das heißt, es können nicht analog zum einführenden Beispiel Gleichungen aufgestellt und die Werte der Koeffizienten berechnet werden. Die Maximierung der Likelihood-Funktion erfolgt deshalb iterativ. Ausgehend von einer anfänglichen Schätzung der Koeffizienten wird diese solange schrittweise verändert, bis sich keine wesentliche Verbesserung des Wertes der Likelihood-Funktion mehr ergibt. Mit den geschätzten Koeffizienten lassen sich dann für jeden Kunden individuelle Kaufwahrscheinlichkeiten entsprechend seiner Ausprägungen der unabhängigen Variablen schätzen bzw. vorhersagen.

Ist nicht eine diskrete Kaufentscheidung, sondern eine stetige Variable wie der Gesamtbetrag, für den nach einem Mailing eingekauft wird, zu erklären, kann ein lineares Regressionsmodell

aufgestellt werden, dessen Koeffizienten zumeist mittels Ordinary Least Squares (OLS)-Schätzung bestimmt werden. Eine ML-Schätzung wäre jedoch ebenso möglich. Unter Annahme der Normalverteilung der zu erklärenden Variable führt diese zu denselben Koeffizienten wie die OLS-Schätzung.

Likelihood-Ratio-Test

Der Likelihood-Ratio-Test ist ein flexibel einsetzbarer Signifikanztest im Rahmen der ML-Schätzung. Er stellt die Likelihood-Werte von zwei Modellen gegenüber, um zu überprüfen, ob sich diese signifikant voneinander unterscheiden. Er ermöglicht damit zum Beispiel die

Überprüfung der Signifikanz einer Einflussgröße, indem eines der beiden Modelle diese nicht enthält, oder die
Überprüfung der Signifikanz des Gesamtmodells, indem eines der beiden Modelle gar keine Einflussgrößen enthält und somit nur das Absolutglied geschätzt wird.

Beitrag aus planung&analyse 14/1 in der Rubrik „Statistik kompakt“

Autoreninformation

Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.

Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.

Literatur

Bortz, J.; Schuster, C.: Methoden der Parameterschätzung. In: Statistik für Human- und Sozialwissenschaftler, 7. Auflage, Berlin, Heidelberg, 2010, S. 90-92.

Frohn, J.: Maximum-Likelihood-Schätzung. In: Grundausbildung in Ökonometrie, Berlin, New York, 1980, S. 81-85.

Zurück zur Übersicht

Share