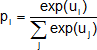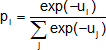Maximum Difference Scaling (MaxDiff)
Maximum Difference Scaling (MaxDiff)
Johannes Lüken / Dr. Heiko Schimmelpfennig
Maximum Difference Scaling (MaxDiff) bzw. Best-Worst-Scaling ist ein Verfahren zur Messung der Wichtigkeit oder Präferenz beispielsweise von Produkteigenschaften, Marken oder Werbeslogans. Im Allgemeinen trennt es besser zwischen den zu beurteilenden Items als entsprechende Abfragen auf einer Ratingskala bzw. vereinfacht die Erhebung im Vergleich zu einer Konstantsummenskala.
Klassisches MaxDiff
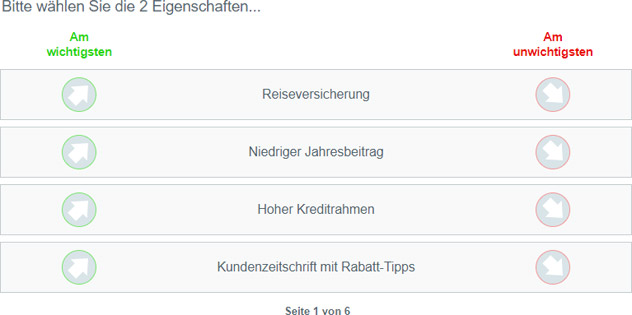
Aus einer vorgegebenen Menge von Items wird jedem Befragten mehrfach eine Teilmenge aus zumeist drei bis fünf Items vorgelegt (siehe Abbildung). Soweit möglich wird jedem Befragten jedes Item durchschnittlich drei Mal vorgelegt und über alle Befragten hinweg annähernd gleich häufig mit jedem anderen kombiniert.
Abbildung: Beispiel einer typischen MaxDiff-Aufgabe
Der Befragte hat jeweils das aus seiner Sicht beste/wichtigste und schlechteste/unwichtigste Item anzugeben. Damit liegt eine Reihe von Informationen über die Items einer einzelnen Aufgabe vor: Bei drei Items je Aufgabe lässt sich eine vollständige und eindeutige Rangfolge dieser drei Items bilden. Bei vier Items liefern die Antworten Informationen zu fünf der sechs möglichen Paarvergleiche. Ist beispielsweise A das wichtigste Item und D das unwichtigste, so ist folglich A > B, A > C, A > D, B > D und C > D, wobei “>” für “wichtiger als” steht. Bei fünf Items je Aufgabe sind noch die Präferenzen von sieben der zehn möglichen Paare definiert.
Ziel der Auswertung der so gewonnenen Daten ist es, für jedes Item i einen Wert ui zu bestimmen, der dessen Nutzen widerspiegelt. Dazu wird ein Logit-Modell zugrunde gelegt, das die Wahrscheinlichkeit liefert, mit der ein Item aus einer Menge von Items
als bestes
bzw. schlechtestes
ausgewählt wird.
Mittels Hierarchical Bayes-Schätzung werden damit für jeden Befragten individuelle Nutzenwerte bestimmt. Dabei fließen nicht nur die eigenen Antworten ein, sondern es werden zur Stabilisierung der Schätzungen auch die Angaben der übrigen Befragten genutzt. Zur besseren Interpretation werden die geschätzten Nutzenwerte anschließend wiederum gemäß Logit-Modell in die erwartete Wahrscheinlichkeit transformiert, mit der ein Item in einer beliebigen Aufgabe als bestes ausgewählt wird. Die sich ergebenden Werte werden schließlich so normiert, dass für jeden Befragten die Summe über alle Items gleich 100 ist.
Anchored MaxDiff
Die (transformierten und normierten) Nutzenwerte eines herkömmlichen MaxDiff können nur in Relation zueinander interpretiert werden. Es kann nicht ausgeschlossen werden, dass beispielsweise alle betrachteten Items eigentlich unwichtig sind. Um einen Rückschluss auf die absolute Wichtigkeit bzw. Präferenz zu ermöglichen, ist die Erhebung zusätzlicher Informationen notwendig. Entweder wird nach jeder einzelnen Aufgabe gefragt, ob alle, einige oder keins der soeben gezeigten Items sehr wichtig sind. Oder am Ende aller Aufgaben wird der Befragte gebeten, aus allen Items diejenigen auszuwählen, die für ihn sehr wichtig sind. Werden diese Angaben bei der Schätzung der Nutzenwerte mit berücksichtigt, repräsentieren positive Nutzenwerte wichtige und negative Nutzenwerte unwichtige Items.
MaxDiffs mit sehr vielen Items
Bei insgesamt 30 zu beurteilenden Items, die jeweils drei Mal vorgelegt werden, und fünf Items je Aufgabe hat ein Befragter 18 (= 30 × 3 / 5) Aufgaben zu bewältigen. Verdoppelt sich die Anzahl an Items, verdoppelt sich auch die Anzahl der notwendigen Aufgaben. Um ein MaxDiff Design mit sehr vielen Items zweckmäßig einsetzen zu können, ist das klassische Vorgehen somit zu modifizieren.
Es wird vorgeschlagen, entweder jedem Befragten (a) nur eine individuelle Auswahl der Items oder (b) jedes Item weniger als durchschnittlich drei Mal vorzulegen. Dadurch verringert sich die Informationsdichte, die für jeden Befragten aufgrund seiner eigenen Antworten vorliegt. Da es das Prinzip der Hierarchical-Bayes-Schätzung ist, fehlende Information aus der Gesamtstichprobe zu gewinnen, ist es insbesondere bei diesen Vorgehensweisen wichtig, dass die Stichprobe bezüglich der Präferenzen weitgehend homogen ist. Falls die Menge an Items nur so groß ist, dass jedes Item jedem Befragten bei einer akzeptablen Menge an Aufgaben mindestens ein Mal vorgelegt werden kann, ist (b) der Option (a) vorzuziehen.
Um die Validität der geschätzten Nutzenwerte zu erhöhen, kann ein Befragter vorab gebeten werden, die Items hinsichtlich seiner Wichtigkeit/Präferenz zu gruppieren. Zum Beispiel hat er aus 80 Items zunächst die wichtigsten 20, aus den verbleidenden 60 wiederum die (nächst)wichtigsten 20 etc. auszuwählen. Erst anschließend wird dann ein MaxDiff Design in der Variante (a) oder (b) durchgeführt. Die Information aus der Gruppierung fließt mit in die MaxDiff Analyse und in (b) auch mit in die Auswahl der Items ein. Allerdings bleibt die Erhebung ähnlich lang wie im klassischen MaxDiff, vermeidet aber eine Monotonie infolge mehrerer Dutzend MaxDiff-Aufgaben.
Beitrag aus planung&analyse 14/4 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter für Multivariate Analysen bei IfaD, Institut für angewandte Datenanalyse, sowie Professor für Betriebswirtschaftslehre an der BiTS, Business and Information Technology School, Hamburg. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung dieser Verfahren verantwortlich und vertritt in der Lehre das Gebiert der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Hendrix, P.; Drucker, S.: Alternative Approaches to MaxDiff with Large Sets of Disparate Items – Augmented and Tailored MaxDiff, Proceedings of the Sawtooth Software Conference, Santa Rosa, 2007, 169-187.
Lattery, K.: Anchoring Maximum Difference Scaling Against a Threshold – Dual Response and Direct Binary Responses, Sawtooth Research Paper Series. Sequim, 2011.
Sawtooth Software: The MaxDiff/Web v6.0 Technical Paper. Sawtooth Software Technical Paper Series. Sequim, 2005-2007.
Wirth, R.; Wolfrath, A.: Using MaxDiff for Evaluating Very Large Sets of Items, Proceedings of the Sawtooth Software Conference, Orlando, 2012, 59-78.
<
Share
