Planung des Stichprobenumfangs
Johannes Lüken / Dr. Heiko Schimmelpfennig
Die Abhängigkeit des Ergebnisses eines Signifikanztests vom Stichprobenumfang führt zu einem Dilemma: Ist der Stichprobenumfang hoch, werden Effekte – zum Beispiel Unterschiede zwischen zwei Mittel- oder Anteilswerten – als signifikant ausgewiesen, obwohl sie aus praktischer Sicht irrelevant sind. Ist er gering, bleiben praktisch relevante Effekte durch einen statistischen Test unerkannt. Gibt man vor, ab welcher Stärke Effekte relevant sind, lässt sich ein optimaler Stichprobenumfang bestimmen, so dass diese Effekte mit einer hohen Wahrscheinlichkeit identifiziert werden.
Der optimale Stichprobenumfang
Einen zu hohen Stichprobenumfang kann es aus statistischer Sicht im Grunde nicht geben. Mit steigender Stichprobengröße wird der zufällige Fehler kleiner und damit die Schätzung von beispielsweise Mittel- oder Anteilswert genauer. Alle signifikanten Effekte können im Nachhinein anhand der Effektstärke in die relevanten und irrelevanten aufgeteilt werden. Um aber unnötige Kosten zu vermeiden, stellt sich die Frage nach dem kleinsten und damit optimalen Stichprobenumfang, der ausreicht, um die praktisch relevanten Effekte zu identifizieren.
Die Power eines Tests bezeichnet die Wahrscheinlichkeit, einen in der Grundgesamtheit vorhandenen Effekt durch den statistischen Test zu erkennen. Diese ist abhängig von Effektstärke, Signifikanzniveau und Stichprobenumfang. Im Allgemeinen gibt man das Signifikanzniveau vor und definiert eine untere Grenze, ab der ein Effekt relevant ist. Zu jedem Stichprobenumfang ergibt sich dann eine bestimmte Power. Der optimale Stichprobenumfang ist der kleinste, der zur Erreichung einer gewünschten Power notwendig ist.
Bestimmung des Stichprobenumfangs
Die Power eines Tests lässt sich einfach mit dem Tool G*Power von Faul et al. (2007) berechnen, indem Signifikanzniveau (zumeist gleich 5%), Effektstärke und Stichprobenumfang angegeben werden. Für den Vergleich der Mittelwerte und von zwei unabhängigen Stichproben ist die Effektstärke definiert durch . Ein kleiner Effekt liegt nach Cohen (1988) in diesem Fall ab d = 0,2 vor. Dieser entspricht beispielsweise bei einer 7-stufigen Rating-Skala einer Differenz der Mittelwerte von 0,3, wenn die beiden Gruppen gleich groß sind und die Standardabweichung der Antworten s = 1,5 beträgt.
Abbildung 1 zeigt die Abhängigkeit der Power vom Stichprobenumfang für einen 2-seitigen t-Test auf Mittelwertunterschiede bei gleich großen Gruppen. Häufig wird als Power 80% gefordert. Um mit dieser Wahrscheinlichkeit auch kleine Effekte aufzudecken, ist 788 der optimale Stichprobenumfang.
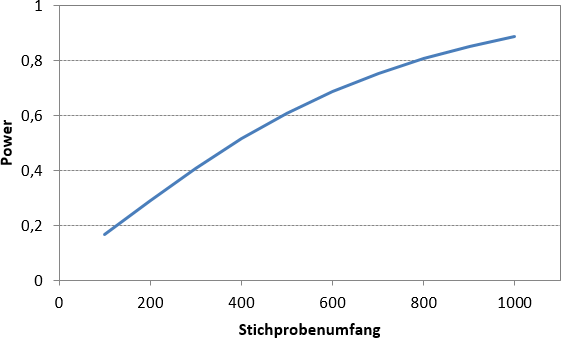Abbildung 1: Entwicklung der Power für den 2-seitigen t-Test mit d = 0,2
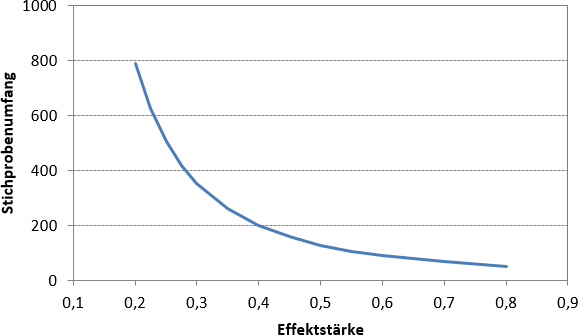
Abbildung 2 veranschaulicht den Einfluss der Effektstärke auf den optimalen Stichprobenumfang für eine Power von 80%. Dieser sinkt mit zunehmender Effektstärke. Ein mittlerer Effekt liegt ab d = 0,5 vor, ein großer ab d = 0,8. Unter gleichen Bedingungen wie zuvor entsprechen diese einer Differenz der Mittelwerte von 0,75 bzw. 1,2. Um einen mittleren Effekt mit einer Wahrscheinlichkeit von 80% zu entdecken, ist ein Stichprobenumfang von 128 nötig. Für einen großen Effekt genügen 52 Befragte.
Abbildung 2: Optimale Stichprobenumfänge für den 2-seitigen t-Test
Für den Vergleich von zwei Anteilswerten p1 und p2 können dieselben Grenzen wie beim Vergleich der Mittelwerte zur Kategorisierung der Effektstärke herangezogen werden, wenn diese durch
mit p2 ≥ p1 gemessen wird. Einem kleinen Effekt von h = 0,2 können zum Beispiel p1 = 0,5 und p2 = 0,6 oder p1 = 0,1 und p2 = 0,17 zugrunde liegen. Um einen kleinen, mittleren oder großen Effekt mittels 2-seitigem z-Test mit einer Wahrscheinlichkeit von 80% zu entdecken, bedarf es derselben Stichprobenumfänge wie beim Vergleich der Mittelwerte.
Beitrag aus planung&analyse 16/6 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Cohen, J.: Statistical Power Analysis for the Behavioral Sciences, 2. Auflage, Hillsdale, 1988.
Faul, F.; Erdfelder, E.; Lang, A.-G.; Buchner, A.: G*Power 3: A Flexible Statistical Power Analysis Program for the Social, Behavioral, and Biomedical Sciences. In: Behavior Research Methods, Jg. 39/2007, 2, S. 175-191.
<
Share
