Latent-Class-Clusteranalyse
Johannes Lüken / Dr. Heiko Schimmelpfennig
Klassische Verfahren der Clusteranalyse weisen ein Objekt eindeutig einem Cluster zu. Ergebnis einer Latent-Class-Clusteranalyse sind dagegen Wahrscheinlichkeiten, mit denen Objekte den einzelnen Clustern zugeordnet werden. Es wird davon ausgegangen, dass latente (nicht beobachtbare) Klassen für Unterschiede in den Daten mit verantwortlich sind.
Einführungsbeispiel
In einer Befragung zur Ermittlung der Präferenzen beim Reisen wurde unter anderem gefragt
- wie Reisen gebucht werden: (a) überwiegend Online / (b) überwiegend Reisebüro / (c) Online & Reisebüro,
- welche Arten von Reisen in Frage kommen: (a) Bildungsreise / (b) Fernreise / (c) Strandurlaub.
Grundsätzlich sind kategoriale Variablen (auch gemeinsam mit Variablen anderer Skalenniveaus) in einer Latent-Class-Clusteranalyse bei Verwendung geeigneter Software einfach zu handhaben. Frage (1) ist eine Einfachnennung und kann mit den Codes 1, 2, und 3 direkt in die Latent-Class-Clusteranalyse übernommen werden. Frage (2) ist eine Mehrfachnennung und somit mit drei dichotomen Variablen zu erfassen. Auf Basis von 1222 Befragten zeigten sich drei Cluster als beste Lösung. In Abbildung 1 sind beispielhaft die individuellen Zuordnungswahrscheinlichkeiten zu den drei Clustern für drei Personen dargestellt, die sich gemäß ihrer Antwortmuster ergeben. Während Person 1 nahezu eindeutig zu Cluster 1 zählt, ist die Zuordnung bei den beiden anderen Befragten nicht ganz so deutlich.
Abbildung 1: Zuordnungswahrscheinlichkeiten
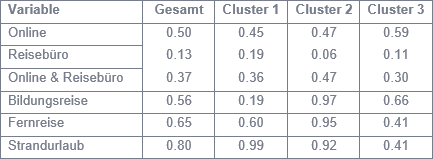
Zur Beschreibung der drei Cluster wird die mit den individuellen Zuordnungswahrscheinlichkeiten gewichtete Häufigkeitsverteilung der Variablen je Cluster ermittelt (siehe Abbildung 2). Cluster 1 ist beispielsweise charakterisiert durch Strandurlauber, die teilweise auch Fernreisen unternehmen und im Vergleich zu den anderen Gruppen am häufigsten im Reisebüro buchen.
Abbildung 2: Profile der Cluster
Grundidee des Verfahrens
Eine Latent-Class-Clusteranalyse liefert genau genommen bedingte Wahrscheinlichkeiten: unter der Bedingung der von einer Person gegebenen Antworten auf die für die Clusteranalyse relevanten Fragen (formal: die in dem Vektor yi gesammelten Werte der entsprechenden Variablen für die Person i) zählt sie mit der Wahrscheinlichkeit zu Cluster 1, mit der Wahrscheinlichkeit zu Cluster 2, etc. „Umgekehrt“ gibt die bedingte Wahrscheinlichkeit an, dass eine Person bestimmte Antworten gibt, unter der Bedingung, dass sie Cluster g angehört. Mit dieser lässt sich die Wahrscheinlichkeit p(yi) berechnen, die Antworten yi zu beobachten. Ist p(g) der Anteil eines Clusters g an der Stichprobe, dann gilt nach dem Satz der totalen Wahrscheinlichkeit
Die bedingte Wahrscheinlichkeit ist bestimmt durch Wahrscheinlichkeitsverteilungen, die für die einzelnen Variablen in Abhängigkeit vom Skalenniveau angenommen werden, und die Parameter, die diese Verteilungen definieren. Die Wahrscheinlichkeit, genau die Antworten aller n Personen einer Stichprobe zu beobachten, ist dann gegeben durch die Likelihood-Funktion
Die Parameter der Verteilungen sowie die Anteile p(g) werden so geschätzt, dass die Likelihood-Funktion maximal wird. Über das Bayes-Theorem lässt sich dann die gesuchte Wahrscheinlichkeit berechnen, dass eine Person i einem Cluster, zum Beispiel g=1 angehört:
Die Schätzung der Likelihood-Funktion wird für verschiedene Clusteranzahlen wiederholt. Anhand von Informationskriterien wie dem Akaike Information Criterion (AIC) oder dem Bayesian Information Criterion (BIC) wird die Auswahl der Clusterlösung getroffen. Je näher der Wert der Likelihood-Funktion an 1 bzw. der Wert der logarithmierten Likelihood-Funktion an 0 liegt, desto besser ist die Schätzung. Da die Informationskriterien auf dem maximalen Wert der logarithmierten Likelihood-Funktion basieren, wird die Clusteranzahl gewählt, für die die Informationskriterien 0 am nächsten kommen.
Beitrag aus planung&analyse 15/5 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Bacher, J., Vermunt, J.K.: Analyse latenter Klassen. In: Wolf, C., Best, H.: Handbuch der sozialwissenschaftlichen Datenanalyse, Wiesbaden, 2010, S. 553-574.
Lüken, J.; Schimmelpfennig, H.: Maximum-Likelihood-Schätzung. In: planung & analyse, Jg. 41/2014, Nr. 1, S. 42.
<