
Kriterien der Prognosegüte für metrische Merkmale
Johannes Lüken / Dr. Heiko Schimmelpfennig
Ziel der Methoden, die unter „Predictive Analytics“ (Predictive Modelling) zusammengefasst werden, ist die Entwicklung von Prognosemodellen, mit denen Ereignisse vorhergesagt oder unbekannte Merkmalswerte bestimmt werden können. Bevor ein Modell genutzt wird, sollte zunächst seine Qualität (für einen Testzeitraum oder anhand einer Validierungsstichprobe) überprüft werden. Dazu bedarf es geeigneter Gütemaße, von denen einige gängige für metrische Merkmale vorgestellt werden.
Ein Prognosemodell soll Marktanteile vorhersagen – beispielsweise die der Top 5 im Lebensmitteleinzelhandel. Die Prognose für 2016 erfolgt mit einer Kleinst-Quadrate (OLS)-Schätzung von linearen Regressionsmodellen auf Basis der Anteile der Jahre 2011 bis 2015 (siehe Abbildung).
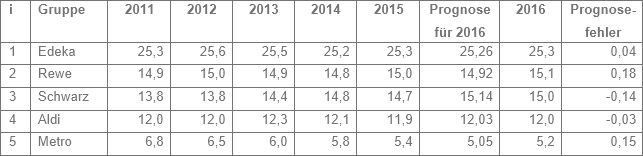
Abbildung: Anteile in % am Lebensmittelumsatz im Einzelhandel in Deutschland (Quelle: Nielsen TradeDimensions, zitiert nach: BVE Jahresberichte)
Für metrische Merkmale basieren die Gütemaße auf dem Prognosefehler bzw. Residuum
![]()
mit
![]()
= tatsächlicher (prognostizierter) Wert für Beobachtung i. Damit sich Über- und Unterschätzungen nicht gegenseitig aufheben, verwendet der Mean Absolute Deviation die Absolutwerte der Prognosefehler
![]()
oder der Mean Square Error die quadrierten Prognosefehler
![]()
mit n = Anzahl der vorhergesagten Beobachtungen. Das Ziehen der Wurzel überführt den MSE wieder in die ursprüngliche Größenordnung und definiert den Root Mean Square Error (RMSE). Aufgrund der Quadrierung wirken sich größere Abweichungen im (R)MSE stärker aus als im MAD, das heißt er ist anfälliger gegenüber Ausreißern.
Für die Prognose auf Basis der OLS-Schätzung sind MAD = 0,11, MSE = 0,02 und RMSE = 0,12. Eine sehr einfache „naive“ Prognose ist in diesem Beispiel die Fortschreibung der Anteile von 2015 für 2016. Für diese sind MAD = 0,14, MSE = 0,03 und RMSE = 0,17. Die naive Prognose ist demnach schlechter. Der Vergleich mit einer anderen Prognose wie der naiven ist im Mean Relative Absolute Error
![]()
bereits integriert. Da für die Edeka-Gruppe der Fehler der naiven Prognose gleich Null ist, kann der MRAE jedoch nicht berechnet werden und es zeigt sich damit ein Nachteil dieses Maßes. Im Vergleich zu MAD und (R)MSE besitzt es aber den Vorteil, dass seine Höhe nicht durch die Größenordnung der Werte beeinflusst wird. Dies gilt grundsätzlich auch für den Mean Absolute Percentage Error
![]()
Die Prognosen auf Basis der OLS-Schätzung weichen durchschnittlich um MAPE = 1,1%, die der naiven Prognose um MAPE = 1,5% von den tatsächlichen Marktanteilen ab. Aufgrund der Division durch den Wert yi wiegen Abweichungen von kleineren tatsächlichen Werten schwerer. Bei sehr kleinen Werten ist der MAPE insofern nicht sinnvoll anwendbar. Dann ist der Weighted Absolute Percentage Error
![]()
geeigneter. Dieser ist für die Prognosemodelle in dem Beispiel gleich 0,7% bzw. gleich 1%. Zum Vergleich: Bei der vergangenen bayerischen Landtagswahl beträgt der WAPE für die 18 Uhr-Prognose der ARD 4,4% und für die vom ZDF 4,8% bezogen auf die sechs im Landtag vertretenen Parteien. Für die Wahl in Hessen ergibt sich ein WAPE von 3,0% bei der ARD und 1,3% beim ZDF.
Beitrag aus planung&analyse 18/6 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Barrot, C.: Prognosegütemaße. In: Albers, S. et al. (Hrsg.): Methodik der empirischen Forschung, 3. Auflage, Wiesbaden, 2009, S. 547-560.
<






