
Kontingenzanalyse und Chi-Quadrat-Test
Johannes Lüken / Dr. Heiko Schimmelpfennig
Besteht ein Zusammenhang zwischen zwei kategorialen Merkmalen? Unterscheiden sich die Verteilungen eines kategorialen Merkmals zwischen zwei oder mehr Gruppen voneinander? Dies sind typische Fragestellungen, die eine Kontingenzanalyse beantwortet. Sie kann auch metrische Merkmale berücksichtigen, wenn die Ausprägungen zu Klassen zusammengefasst werden.
Messung der Stärke des Zusammenhangs
Ein Beispiel: Es wurde die ungestützte Erinnerung an die Werbung für eine Marke erhoben. Untersucht werden soll, ob es einen Zusammenhang zwischen der Erinnerung und dem Alter gibt, das heißt ob sich der Anteil derjenigen, die sich an die Werbung erinnern, zwischen den Altersgruppen unterscheidet. Die Kontingenztabelle zeigt in schwarz das Ergebnis einer Befragung von 500 Personen. Beispielsweise haben 5 der 18- bis 29-Jährigen die Werbung erinert, 75 nicht. Das Verhältnis von erinnerter Werbung zu nicht erinnerter Werbung beträgt in dieser Gruppe 1:15, in der Gruppe der 30- bis 49-Jährigen 1:3 und in der Gruppe der ≥ 50-Jährigen 1:5. Die Unterschiede deuten auf eine Abhängigkeit der beiden Merkmale hin.
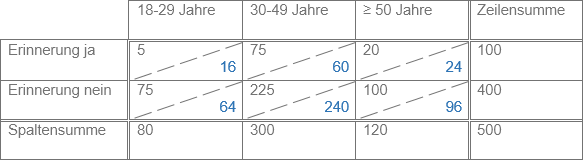
Abbildung: Beobachtete / erwartete absolute Häufigkeiten
Vollkommene Unabhängigkeit läge vor, wenn die Verhältnisse in allen Altersgruppen gleich sind. Für die in blau dargestellten Häufigkeiten ist dies der Fall. Das Verhältnis ist immer 1:4. Diese bei Unabhängigkeit zu erwartenden Häufigkeiten lassen sich je Zelle gemäß
Zeilensumme · Spaltensumme / Stichprobenumfang
bestimmen, so dass Zeilen- und Spaltensummen unverändert bleiben. Je größer die Abweichungen der beobachteten (fb) von den erwarteten Häufigkeiten (fe) sind, desto stärker ist der Zusammenhang zwischen beiden Merkmalen. Um die Stärke des Zusammenhangs zu quantifizieren, wird je Zelle (fb – fe)² / fe berechnet. Die Summe dieser Werte über alle Zellen wird zumeist als χ² bezeichnet und ist in dem Beispiel gleich 14,974. Auf dessen Basis sind verschiedene Zusammenhangsmaße definiert. Mit n als Stichprobenumfang ist der
![]()
In dem Beispiel beträgt er 0,171. Generell ist sein Minimum gleich 0 und sein Maximum gleich![]()
, wenn k und l der Anzahl der Kategorien der beiden Merkmale entsprechen. Damit eine Interpretation vor dem Hintergrund des gängigen Wertebereichs von 0 (≙ vollkommene Unabhängigkeit) bis 1 (≙ totale Abhängigkeit) möglich ist, erfolgt eine Multilplikation mit dem Kehrwert des Maximums und es ergibt sich der
![]()
Explizit als Maß für die Effektstärke (für die Relevanz eines Effekts) gilt![]()
Nach Cohen (1988) ist ein Effekt ab 0,1 klein, ab 0,3 mittel und ab 0,5 groß. In diesem Beispiel ist Cohens w = 0,173 und damit der Effekt eher klein.
Chi²-Test
Ob ein Zusammenhang zwischen zwei Merkmalen oder Unterschiede in den Verteilungen nicht allein auf den Zufall zurückzuführen sind, wird mit dem Chi²-Test überprüft. Dessen Name ist angelehnt an die Teststatistik χ², die mit steigendem Stichprobenumfang näherungsweise Chi²-verteilt ist mit (k-1)·(l-1) Freiheitsgraden. Die Freiheitsgrade entsprechen der Anzahl Zellen, die frei variierbar sind, wenn die Zeilen- und Spaltensummen feststehen. Das heißt in einer 2×3-Kontingenztabelle können zwei Werte beliebig vorgegeben werden. Dann sind die Werte der restlichen vier Zellen eindeutig bestimmt.
Der p-Wert – die Wahrscheinlichkeit, die Hypothese „Es besteht kein Zusammenhang (zwischen Erinnerung und Alter)“ fälschlicherweise abzulehnen – lässt sich beispielsweise mit Hilfe der Excel-Funktion CHIQU.VERT.RE(χ²; (k-1)·(l-1)) bestimmen. Im Beispiel ist p = 0,0006 = 0,06% und damit deutlich kleiner als das übliche Signifikanzniveau von α = 5%. Insofern wird die Hypothese abgelehnt; der Zusammenhang bzw. die Unterschiede sind signifikant.
Um herauszufinden, zwischen welchen Altersgruppen die Unterschiede signifikant sind, erfolgen analog zur Varianzanalyse paarweise Chi²-Tests mit Anpassung des Signifikanzniveaus aufgrund der alpha-Fehler-Kumulierung (siehe Lüken/Schimmelpfennig 2017). Bei Verwendung der Bonferroni-Korrektur ist das angepasste Signifikanzniveau gleich Signifikanzniveau / Anzahl der Paarvergleiche. Im Beispiel ist es 0,05/3 = 0,017. Die p-Werte der drei paarweisen Tests sind:
18 bis 29 Jahre vs. 30 bis 49 Jahre: p = 0,0003
18 bis 29 Jahre vs. ≥ 50 Jahre : p = 0,0291
30 bis 49 Jahre vs. ≥ 50 Jahre : p = 0,0654
Nur für den Vergleich der Gruppe der 18- bis 29-Jährigen mit der der 30- bis 49 Jährigen ist p < 0,017 und damit der Unterschied signifikant.
Als Faustregel für die Anwendbarkeit des Chi²-Tests gilt, dass nicht mehr als 20% der Zellen eine erwartete absolute Häufigkeit kleiner als fünf und keine Zelle eine kleinere als eins haben sollten. Je nach Größe der Kontingenztabelle kommen ansonsten verschiedene alternative Tests in Betracht (siehe Bortz et al. 2008).
Beitrag aus planung&analyse 18/1 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Bortz, J.; Lienert, G. A.; Boehnke, K.: Analyse von Häufigkeiten. In: Verteilungsfreie Methoden der Biostatistik, 3. Auflage, Berlin, Heidelberg, 2008, S. 87-196.
Cohen, J.: Statistical Power Analysis for the Behavioral Sciences, 2. Auflage, Hillsdale, 1988.
Lüken, J.; Schimmelpfennig, H.: Einfaktorielle Varianzanalyse In: planung&analyse, Nr. 2/2017, S. 73.
<






