Klassifizieren mittels Diskriminanzanalyse
Johannes Lüken / Dr. Heiko Schimmelpfennig
Zu den Aufgaben der Diskriminanzanalyse zählt die Identifikation der Eigenschaften, hinsichtlich der sich Objekte verschiedener Gruppen unterscheiden (siehe Blog-Beitrag „Diskriminanzanalyse“). Größere praktische Bedeutung besitzt sie jedoch als Klassifizierungs- bzw. Allokationstool, dessen Ziel in der Zuordnung von Objekten mit unbekannter Gruppenzugehörigkeit zu den vorgegebenen Gruppen besteht.
Typisches Beispiel für das Klassifizieren (neuer) Objekte
Häufig ist die Gruppenzugehörigkeit das Resultat einer Clusteranalyse. Personen, die nicht Teil der Clusteranalyse waren, lassen sich nachträglich mithilfe der Diskriminanzanalyse den Segmenten zuordnen, wenn bei ihnen zumindest die diskriminatorisch bedeutendsten Eigenschaften erhoben werden. Auf diese Weise können zudem bei nachfolgenden Befragungen die Teilnehmer nach ihrer Zugehörigkeit zu diesen Segmenten quotiert werden.
Klassifikationskonzepte
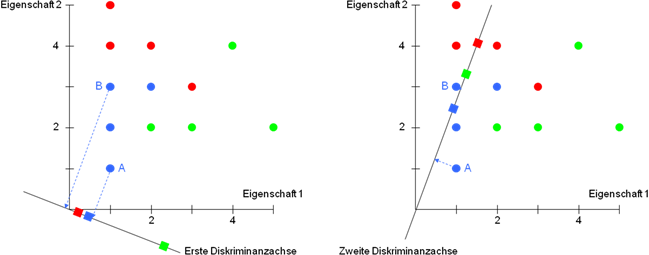
Zur Veranschaulichung von zwei Ansätzen zur Klassifikation wird das Beispiel aus dem letzten Beitrag dieser Reihe aufgegriffen. Abbildung 1 zeigt zwölf Objekte, die anhand von zwei Eigenschaften beschrieben und drei Gruppen zugeordnet sind. Somit können 3 – 1 = 2 Diskriminanzfunktionen extrahiert werden. Das grafische Pendant zur Diskriminanzfunktion ist die Diskriminanzachse. Auf ihr lassen sich die Werte der jeweiligen Diskriminanzfunktion der einzelnen Objekte abtragen, indem das Lot von einem Objekt auf die Diskriminanzachse gefällt wird. Auf diesen Diskriminanzwerten basiert das Distanzkonzept zur Klassifikation von Objekten:
Ein Objekt wird der Gruppe zugeordnet, für die die Distanz zwischen dem Diskriminanzwert des Objekts und dem Gruppenzentroid minimal ist.
Ein Gruppenzentroid ist das arithmetische Mittel der Diskriminanzwerte der Objekte einer Gruppe. Diese sind in Abbildung 1 durch ¢, ¢ und ¢ dargestellt. Betrachtet man nur die erste Diskriminanzfunktion bzw. -achse, so wird beispielsweise Objekt A der blauen Gruppe zugordnet, da sein Diskriminanzwert dem Mittel ¢ am nächsten liegt. Objekt B wird jedoch fälschlicherweise der roten Gruppe zugewiesen. Die zweite Diskriminanzfunktion bzw. -achse ordnet A ebenfalls der blauen Gruppe zu, B jedoch jetzt der grünen Gruppe und somit wiederum falsch. Berücksichtigt man gleichzeitig beide Diskriminanzfunktionen, indem die Summe der Distanzen zur Klassifikation herangezogen wird, so wird B der blauen und damit richtigen Gruppe zugeordnet, da bei der ersten Diskriminanzfunktion die Distanz zur grünen Gruppe und bei der zweiten die Distanz zur roten Gruppe sehr groß ist.
Die Bestimmung eigener Klassifizierungsfunktionen für jede Gruppe ist ein weiterer Ansatz zur Klassifikation, der ohne die Bestimmung von Diskriminanzfunktionen bzw. -werten auskommt. Die Berechnung der Funktionskoeffizienten basiert auf den Mittelwerten und den (Ko-)Varianzen der Eigenschaften innerhalb der Gruppen. Für das Beispiel ergeben sich mit x1 und x2 als Variablen für die beiden Eigenschaften folgende Klassifizierungsfunktionen:
Fblau = -4,97 + 1,40∙x1 + 2,66∙x2
Frot = -12,26 + 1,99∙x1 + 4,71∙x2
Fgrün = -11,52 + 3,80∙x1 + 3,03∙x2
Zur Klassifizierung eines Objekts werden dessen Eigenschaftsausprägungen in alle Funktionen eingesetzt. Es wird dann der Gruppe mit dem höchsten Wert der Klassifizierungsfunktion zugeordnet. Sind die Gruppen in der Realität unterschiedlich groß, ist die Wahrscheinlichkeit, dass ein Objekt zu einer größeren Gruppe gehört, a priori höher als zu einer kleineren zu zählen. Klassifizierungsfunktionen berücksichtigen a priori Wahrscheinlichkeiten P(g) zu einer Gruppe g zu gehören durch Addition des natürlichen Logarithmus von P(g), wobei P(g) zum Beispiel die relative Häufigkeit ist, mit der Gruppe g in der Stichprobe auftritt.
Sowohl die Werte der Klassifizierungsfunktionen wie auch die Distanzen lassen sich in Wahrscheinlichkeiten der Zugehörigkeit zu den Gruppen transformieren und ermöglichen somit auch eine probabilistische anstelle der deterministischen Zuordnung.
Abbildung 1: Bestimmung der Diskriminanzwerte der beiden Diskriminanzfunktionen
Güte der Klassifikation
In einer Klassifikationsmatrix werden die Ergebnisse der Klassifizierung der tatsächlichen Gruppenzugehörigkeit gegenübergestellt. Auf der Hauptdiagonalen ist abzulesen, wie viele Objekte korrekt zugeordnet werden. Abbildung 2 zeigt, dass nur mit der ersten extrahierten Diskriminanzfunktion die Klassifikation für sieben der zwölf Objekte gelingt. Dies entspricht einer Trefferquote von 58,3%. Werden beide Diskriminanzfunktionen genutzt, so erhöht sie sich auf 75%. Die Klassifizierungsfunktionen ohne Berücksichtigung von a priori Wahrscheinlichkeiten führen stets zu demselben Ergebnis wie das Distanzkonzept auf Basis aller Diskriminanzfunktionen.
Abbildung 2: Klassifikationsmatrix für die erste Diskriminanzfunktion und für beide Diskriminanzfunktionen
Eine für die Beurteilung der Eignung von Diskriminanz- oder Klassifizierungsfunktionen als Allokationstool verlässliche Trefferquote ergibt sich nur, wenn nicht alle Fälle einer Stichprobe zur Bestimmung der Diskriminanz- oder Klassifizierungsfunktionen auch selber wieder klassifiziert werden. Die Stichprobe ist stattdessen in eine Trainings- und eine Teststichprobe aufzuteilen. Klassifiziert werden dann analog zur späteren Anwendung nur die Fälle der Teststichprobe, das heißt die Fälle, die nicht in die Schätzung der Koeffizienten der Funktionen eingegangen sind. Die Trefferquote sollte die relative Häufigkeit überschreiten, mit der die größte Gruppe in der Teststichprobe vertreten ist. Denn diese ist auch ohne irgendeine Analyse zu erreichen, wenn alle Objekte eben dieser Gruppe zugeordnet werden.
Beitrag aus planung&analyse 16/1 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Backhaus, K.; Erichson, B.; Plinke, W.; Weiber, R.: Diskriminanzanalyse. In: Multivariate Analysemethoden, 13. Auflage, Berlin, 2011, S. 187-248.
Decker, R.; Rašković, S.; Brunsiek, K.: Diskriminanzanalyse. In: Wolf, C.; Best, H. (Hrsg.): Handbuch der sozialwissenschaftlichen Datenanalyse, Wiesbaden, 2010, S. 495-523.
<