Kategoriale Variablen in Regressionsmodellen
Johannes Lüken / Dr. Heiko Schimmelpfennig
Regressionsmodelle sind nicht beschränkt auf metrische unabhängige Variablen. Kategoriale Variablen wie Geschlecht, Beruf etc. können Berücksichtigung finden, wenn ihre Ausprägungen als Zahlen dargestellt werden. Eine gängige Vorgehensweise ist die Dummy-Codierung.
Dummy-Codierung unabhängiger dichotomer Variablen
Es soll untersucht werden, welchen Einfluss neben dem Preis das Schalten einer Werbung auf den monatlichen Absatz besitzt. Die lineare Regressionsfunktion ist somit
Absatzmenge = b0 + b1×Preis + b2×Werbung
Während der Preis eine metrische Variable ist, weist die Werbung nur zwei Kategorien auf: es wurde eine Werbung (zu Beginn eines Monats) geschaltet oder nicht. Um diese Einflussgröße im Regressionsmodell zu berücksichtigen, sind beiden Ausprägungen Zahlen zuzuordnen. Folgt man der Dummy-Codierung, ist einer Referenzkategorie der Wert 0 und der anderen Kategorie der Wert 1 zu geben. In diesem Beispiel bietet es sich an, als Referenzkategorie den Verzicht auf Werbung festzulegen. Der Regressionskoeffizient b2 gibt dann genau die Menge an, um die sich der Absatz durch das Schalten einer Werbung gegenüber der Referenzkategorie „keine Werbung“ bei konstantem Preis verändert.
Dummy-Codierung unabhängiger Variablen mit mehr als zwei Kategorien
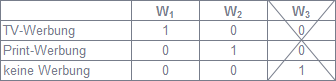
Es wird zusätzlich differenziert, ob eine TV- oder Print-Werbung geschaltet wurde. Insofern sind drei Kategorien zu unterscheiden. Damit bedarf es zur Codierung der zwei Variablen W(erbung)1 und W(erbung)2 (siehe Abbildung 1).
Die Kombination der Variablen mit den Ausprägungen W1 = 1, W2 = 0 repräsentiert somit TV-Werbung, W1 = 0, W2 = 1 Print-Werbung und W1 = 0, W2 = 0 keine Werbung. Durch diese Kombinationen sind alle drei Kategorien eindeutig definiert. Eine dritte Variable W3 wäre nicht nur redundant, sondern würde zu exakter Multikollinearität führen, so dass das Regressionsmodell nicht schätzbar wäre. „Keine Werbung“ ist auch hier die Referenzkategorie, da für diese beide Codiervariablen gleich 0 sind. In der entsprechenden Regressionsfunktion
Absatzmenge = b0 + b1×Preis + b2×W1 +b3×W2
quantifizieren b2 und b3 die Wirkungen der TV- bzw. Print-Werbung auf die Absatzmenge im Vergleich zur Referenzkategorie. Die Differenz zwischen b2 und b3 gibt an, um wie viel sich die Wirkung einer Werbung zwischen den beiden Medien unterscheidet.
Interaktionseffekte mit kategorialen Variablen
Die Interpretation der Regressionskoeffizienten geht davon aus, dass keine Mehrfachnennungen für die kategoriale Variable vorliegen. Das heißt, es darf im selben Monat nicht in TV und Print geworben worden sein. Um auch den Effekt einer gemeinsamen Werbung in beiden Medien zu bestimmen, ist eine eigene zusätzliche Kategorie „TV & Print“ zu berücksichtigen (siehe Abbildung 2).
Alternativ lassen sich TV-Werbung (ja/nein) und Print-Werbung (ja/nein) als zwei eigenständige dichotome Variablen auffassen. Geht man davon aus, dass gleichzeitige Werbung in beiden Medien nicht additiv wirkt, besteht zwischen diesen ein Interaktionseffekt. Dieser kann durch Aufnahme des Produkts der beiden Variablen im Modell abgebildet werden:
Absatzmenge = b0 + b1×Preis + b2×TV +b3×Print + b4×TV×Print
Die Wirkung einer gemeinsamen Werbung ist dann gleich der Summe der Einzeleffekte und des Interaktionseffekts (b2 + b3 + b4). Diese entspricht dem Regressionskoeffizienten der Codiervariable W3 aus Abbildung 2, falls TV & Print-Werbung als eigene Kategorie dargestellt wird.
Abbildung 2: Dummy-Codierung bei Mehrfachnennungen
Ebenso kann ein Interaktionseffekt zwischen Werbung und Preis, das heißt zwischen einer kategorialen und einer metrischen Variable, im Modell berücksichtigt werden. Im einführenden Beispiel der Dummy-Codierung der dichotomen Variable Werbung wird ihr Produkt mit dem Preis in die Regressionsfunktion aufgenommen:
Absatzmenge = b0 + b1×Preis + b2×Werbung +b3×Preis×Werbung
Angenommen, der Zusammenhang zwischen Preis und Absatzmenge ist negativ (b1 < 0), so bedeutet ein negativer Koeffizient b3, dass die Wirkung des Preises auf den Absatz bei Schalten einer Werbung stärker ist als ohne Werbung. Ein positiver Koeffizient deutet dagegen auf geringere Preissensibilität hin.
Neben der Dummy-Codierung sind die Effekt- und die Kontrast-Codierung übliche Vorgehensweisen. Die Art der Codierung beeinflusst zwar die Regressionskoeffizienten und deren Interpretation. Das Bestimmtheitsmaß und damit Ergebnisse der Prüfungen der Signifikanz von Verbesserungen des Bestimmtheitsmaßes infolge der Berücksichtigung weiterer Variablen oder von Interaktionseffekten sind davon jedoch unabhängig.
Beitrag aus planung&analyse 13/5 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Cohen, J.; Cohen, P.; West, S. G.; Aiken, L. S.: Interactions With Categorical Variables, In: Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences, 3. Auflage, Mahwah, New Jersey, 2003, S. 354-389.
Eid, M.; Gollwitzer, M.; Schmitt, M.: Multiple Regressionsanalyse, In: Statistik und Forschungsmethoden, 2. Auflage, Weinheim, Basel, 2011, S. 648-677.
<