Interaktionseffekte in Kausalanalysen
Johannes Lüken / Dr. Heiko Schimmelpfennig
Interaktionen bzw. Wechselwirkungen zwischen unabhängigen Variablen liegen in einer Kausalanalyse vor, wenn sich Variablen in ihrer Wirkung auf eine abhängige Variable gegenseitig verstärken oder abschwächen. Häufig wird beispielsweise berichtet, dass reiche Menschen gesünder sind als arme und sich dieser Unterschied mit zunehmendem Alter vergrößert. Das Alter verstärkt demnach den Einfluss des Einkommens auf die Gesundheit. Eine Berücksichtigung von Interaktionen kann Vorhersagen somit deutlich verbessern.
Interaktion zwischen zwei Variablen
Ein lineares Regressionsmodell zur Untersuchung der Zusammenhänge zwischen der abhängigen Variable y und zwei unabhängigen Variablen x1 und x2, das keine Interaktion berücksichtigt, lässt sich formal schreiben als
y = b0 + b1×x1 +b2×x2
Die Regressionskoeffizienten b1 und b2 quantifizieren die Einflussstärken der Variablen. Die Stärke des Einflusses von x1 ist immer gleich b1 – gleichgültig welche Ausprägung x2 aufweist. Liegt dagegen ein Interaktionseffekt vor, verändert sich die Einflussstärke von x1 (im einführenden Beispiel das Einkommen), wenn sich x2 (das Alter) ändert. Um diese Abhängigkeit zu erfassen, wird die Einflussstärke von x1 zusätzlich zu b1 durch den Term b3×x2 gemessen:
y = b0 + (b1 + b3×x2)×x1 + b2×x2 (*)
Grafisch lassen sich die beiden Situationen anhand von Regressionsgeraden veranschaulichen, die die Beziehung zwischen x1 und der abhängigen Variable jeweils für zwei unterschiedliche Ausprägungen von x2 zeigt (siehe Abbildung).
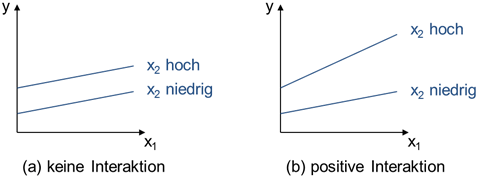Abbildung: Regressionsgeraden für verschiedene Werte von x2
Wird keine Interaktion berücksichtigt bzw. liegt keine Interaktion vor, verlaufen beide Regressionsgeraden parallel zueinander. Die Steigungen respektive Einflussstärken sind gleich – egal ob der Wert von x2 hoch oder niedrig ist. Nur aufgrund des größeren Wertes von x2 befindet sich die eine Regressionsgerade auf einem höheren Niveau. Bei einer positiven Interaktion ist die Regressionsgerade für den größeren Wert von x2 dagegen steiler. Allgemein ist die Einflussstärke von x1 umso höher, je größer x2 ist.
Interaktionseffekte sind nicht einseitig, sondern immer wechselseitig. Die Möglichkeit der Transformation der Gleichung (*) zu
y = b0 + b1×x1 + (b2 + b3×x1)×x2
verdeutlicht, dass (b2 + b3×x1) die Einflussstärke von x2 misst. Die Einflussstärken können folglich nicht generell, sondern nur unter Vorgabe bestimmter Werte für x1 respektive x2 angegeben werden. Insofern kann ein Test der Signifikanz beispielsweise des Einflusses von x1 unter Berücksichtigung eines Interaktionseffekts immer nur für einen bestimmten Wert von x2 erfolgen. Auf diese Weise lassen sich Bereiche für x2 bestimmen, innerhalb derer der Einfluss von x1 signifikant ist.
Schätzung des Modells
Das Ausmultiplizieren der Klammern in Gleichung (*) führt zu
y = b0 + b1×x1 + b2×x2 + b3×x1×x2
Um eine mögliche Interaktion in einem Regressionsmodell zu berücksichtigen, wird dieses ergänzt um das Produkt der beiden Variablen. Das heißt das Modell enthält eine weitere Variable, deren Werte sich durch Multiplikation von x1 und x2 ergeben. Die Koeffizienten können dann mithilfe der üblichen Ordinary Least Squares (OLS)-Schätzung bestimmt werden. Ob der Interaktionseffekt signifikant ist, lässt sich durch Prüfung der Signifikanz des Koeffizienten b3 oder der Erhöhung des Bestimmtheitsmaßes im Vergleich zum Modell ohne Interaktion bestimmen.
Zentrieren unabhängiger metrischer Variablen
Die Einflussstärke einer Variable in dem Modell mit Interaktion entspricht nur dann genau ihrem Regressionskoeffizienten, wenn die andere Variable gleich null ist. Dessen Interpretation ist insofern häufig wenig aussagekräftig. Repräsentiert x2 zum Beispiel das Alter, so wäre b1 die Einflussstärke von x1 für diejenigen, die 0 Jahre alt sind. Erleichtert wird die Interpretation, wenn die unabhängigen Variablen vorab zentriert werden. Das heißt von jedem Wert einer Variable wird der Mittelwert dieser Variable subtrahiert. Eine zentrierte Variable ist somit immer gleich null, wenn ihr ursprünglicher Wert dem Mittelwert entspricht. Dann gibt b1 die Einflussstärke von x1 für das durchschnittliche Alter in der Stichprobe an.
Das Zentrieren besitzt noch einen weiteren Vorteil. In einem Modell mit Interaktion korrelieren x1 und x2 hoch mit der Variable, die aus dem Produkt beider Variablen gebildet wird. Insofern sind die geschätzten Koeffizienten aufgrund hoher Multikollinearität verzerrt. Das Zentrieren der Variablen vor ihrer Multiplikation vermindert das Ausmaß an Multikollinearität und damit Verzerrungen erheblich.
Interaktionen bei mehr als zwei Variablen
Enthält ein Modell mehr als zwei unabhängige Variablen, kann zum einen die Interaktion zwischen drei oder mehr Variablen untersucht werden. Analog zu einer paarweisen Interaktion wird das Produkt der entsprechenden Variablen in das Regressionsmodell aufgenommen. Zum anderen lassen sich verschiedene paarweise Interaktionen betrachten. Allerdings kann mit der Berücksichtigung mehrerer Produktterme im Modell die Multikollinearität trotz Zentrierens wieder zu einem größeren Problem werden. Dann ist es zwar möglich, das Gesamtmodell zur Vorhersage zu nutzen, die einzelnen Effekte können aber nicht valide bestimmt werden.
Beitrag aus planung&analyse 13/4 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Cohen, J.; Cohen, P.; West, S. G.; Aiken, L. S.: Interactions Among Continuous Variables, In: Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences, 3. Auflage, Mahwah, New Jersey, 2003, S. 255-291.
<
Share
