Induktion von Entscheidungsbäumen mit CHAID
Johannes Lüken / Dr. Heiko Schimmelpfennig
Zu den bekanntesten Algorithmen für das Aufstellen von Entscheidungsbäumen zählt CHAID (Chi-squared Automatic Interaction Detector). Ein solcher Entscheidungsbaum veranschaulicht die hierarchische Aufteilung eines Datensatzes in immer homogener werdende Teilgruppen. Am Beispiel einer Kundenzufriedenheitsanalyse wird das Verfahren vorgestellt und gezeigt, wie Kombinationen von Variablen ermittelt werden, die Segmente zufriedener und unzufriedener Kunden definieren.
(Fiktives) Beispiel
Von 1100 Kunden eines Online-Shops wurde neben der Gesamtzufriedenheit die Zufriedenheit mit dem Bestellvorgang, dem Sortiment, der Lieferzeit und der Reklamationsabwicklung auf einer Skala mit den Kategorien „zufrieden“, „weder/noch“ und „unzufrieden“ erhoben. Hatte jemand mit der Reklamationsabwicklung bislang keine Erfahrungen gemacht, sollte keine der drei Kategorien angegeben werden. Somit resultierende fehlende Werte können in CHAID eine eigene Kategorie einer Variable darstellen und müssen nicht ersetzt oder die Fälle gänzlich gestrichen werden. Insgesamt zeigte sich, dass 61 % der Kunden mit dem Shop zufrieden, 18 % unzufrieden und 21 % weder zufrieden noch unzufrieden sind.
Algorithmus
Im Wesentlichen besteht der CHAID-Algorithmus aus zwei Schritten:
- Für jede unabhängige Variable (mit mehr als zwei Kategorien) Zusammenfassung der Kategorien, die sich hinsichtlich der abhängigen Variable nicht signifikant unterscheiden; bei ordinalen Variablen wird berücksichtigt, dass nur benachbarte Kategorien zusammengefasst werden können
- Auswahl der Trennungsvariable, das heißt der Variable mit dem stärksten Zusammenhang mit der abhängigen Variable gemessen durch den p-Wert eines Chi²-Tests
Die ursprünglichen beziehungsweise zusammengefassten Kategorien der Trennungsvariable bilden dann Knoten (Teilgruppen) des Entscheidungsbaums. In den Untergruppen werden wiederum die Schritte (1.) und (2.) durchlaufen. Gibt es keine Variable, die signifikant mit der abhängigen Variable zusammenhängt, oder würden die entstehenden Untergruppen eine vorgegebene Mindestgröße unterschreiten, erfolgt keine (weitere) Verzweigung.
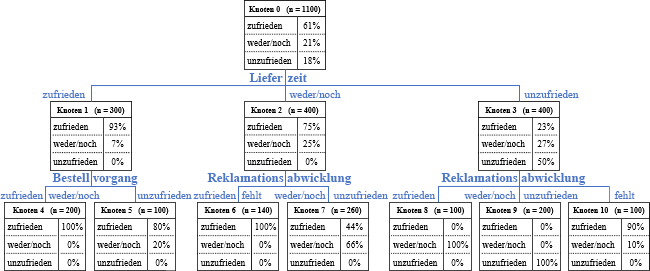
Der Entscheidungsbaum für das Beispiel zeigt, dass die Lieferzeit am stärksten mit der Gesamtzufriedenheit zusammenhängt. Da auf der ersten Ebene die Gesamtheit in drei Teilgruppen entsprechend der Kategorien dieser Variable aufgespaltet wird, fand eine Zusammenfassung von Kategorien zuvor nicht statt. Die Gruppe der mit der Lieferzeit Zufriedenen wird anhand des Bestellvorgangs, die anderen beiden Gruppen anhand der Reklamationsabwicklung weiter unterteilt. Dabei erfolgt zum Beispiel eine Zusammenfassung der Kategorien „zufrieden“ und Angabe „fehlt“ für die Gruppe derjenigen, die mit der Lieferzeit weder zufrieden noch unzufrieden sind. Man erhält schließlich Segmente, die hinsichtlich der Gesamtzufriedenheit möglichst homogen sind und infolge einer zu Beginn gemachten Vorgabe mindestens 100 Fälle umfassen. Die Zufriedenheit mit dem Sortiment trägt bis zu dieser Ebene nicht zur Differenzierung zwischen den Segmenten bei.
Abbildung: Entscheidungsbaum
Interpretation der Endknoten (Segmente)
Ein Kunde ist…
… zufrieden, wenn er mit der Lieferzeit zufrieden ist (Knoten 4 und 5)
… zufrieden, wenn er mit der Lieferzeit zwar weder zufrieden noch unzufrieden ist, aber keine Reklamation nötig war oder er mit der Reklamation zufrieden ist (Knoten 6); ansonsten ist er zumindest nicht unzufrieden (Knoten 7)
… zufrieden trotz Unzufriedenheit mit der Lieferzeit, wenn keine Reklamation notwendig war (Knoten 10)
… weder zufrieden noch unzufrieden, da sich die Unzufriedenheit mit der Lieferzeit trotz zufriedenstellender Reklamationsabwicklung nicht völlig vergessen lässt (Knoten 8)
… nur dann unzufrieden, wenn er mit der Lieferzeit unzufrieden ist und die Reklamationsabwicklung ihn nicht zufrieden gestellt hat (Knoten 9)
Erweiterung für metrische Variable
Der Fokus von CHAID liegt auf der Analyse kategorialer (nominaler oder ordinaler) Variablen. Metrische unabhängige Variablen können berücksichtigt werden, sind aber vor der eigentlichen Analyse in Klassen einzuteilen. Bei einer metrischen abhängigen Variable kann zur Bestimmung des p-Wertes anstelle des Chi²-Tests ein F-Test analog zur einfaktoriellen Varianzanalyse verwendet werden.
Beitrag aus planung&analyse 17/6 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Musiol, G.; Steinkamp; G.: CHAID – Ein Instrument für die empirische Marktforschung. In: Hippner, H.; Meyer, M.; Wilde, K.D. (Hrsg.): Computer Based Marketing, Braunschweig, Wiesbaden, 1998, S. 581-590.
<