Hierarchische Clusteranalyse

Johannes Lüken / Dr. Heiko Schimmelpfennig

Neben den partitionierenden zählen die hierarchischen Verfahren zu den bedeutendsten Methoden der Clusteranalyse. Sie fassen die zu gruppierenden Elemente schrittweise zu immer größeren Clustern zusammen. Dagegen gehen partitionierende Verfahren von einer gegebenen Klassifikation der Elemente aus und versuchen diese durch Umgruppierungen zu verbessern.

 

Verfahren der Hierarchischen Clusteranalyse

Hierarchische Verfahren werden unterteilt in agglomerative und divisive Algorithmen. Praktische Relevanz besitzt jedoch nur die agglomerative Vorgehensweise. Im Fall einer deterministischen Clusteranalyse mit Objekten beinhaltet sie folgende Schritte:

1. In der Ausgangslösung ist jedes Objekt ein eigenständiges Cluster.
2. Die zwei ähnlichsten Cluster werden sukzessive zu einem neuen Cluster zusammengefasst, bis sich alle Objekte in einem Cluster befinden.

Eine Folge dieses Vorgehens ist, dass einmal zu einem Cluster zusammengefasste Elemente im weiteren Fusionsprozess nicht mehr voneinander getrennt werden können. Durch die Veränderung der Cluster aufgrund der Hinzunahme weiterer Elemente kann es passieren, dass ein Objekt letztlich nicht mehr dem Cluster zugeordnet ist, zu dessen anderen Elementen es am ähnlichsten ist.

Es existiert eine Reihe verschiedener agglomerativer Algorithmen, die sich im Hinblick auf die Bestimmung der Ähnlichkeit zwischen zwei Clustern unterscheiden. Abbildung 1 zeigt ein kleines Datenbeispiel mit vier Objekten, die anhand von zwei Merkmalen charakterisiert sind. Beispielsweise könnte die Ähnlichkeit der beiden Cluster {O₁,O₂} und {O₃,O₄} in Abbildung 1d durch die beiden Objekte aus den zwei Clustern bestimmt sein, die sich

• am nächsten sind, d.h. O₁ und O₃ (Single-Linkage Verfahren), oder
• am weitesten entfernt voneinander sind, d.h. O₂ und O₄ (Complete-Linkage Verfahren).

Ein weiteres, nämlich das Ward-Verfahren gilt unter üblichen Rahmenbedingungen als die beste Methode.

 

Ward-Verfahren

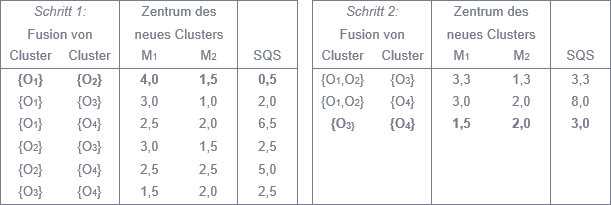
Zentral für das Ward-Verfahren ist die Streuungsquadratsumme (SQS) einer Klassifikation. Formal ist diese bestimmt durch die quadrierten Abweichungen der Objekte eines Clusters zum Clusterzentrum (= Mittelwerte der Objekte eines Clusters) summiert über alle Cluster. Grafisch bedeutet die SQS beispielsweise für die Klassifikation in Abbildung 1d: die (euklidischen) Distanzen vom Clusterzentrum · zum Objekt O₃ und zum Objekt O₄ sowie die (euklidischen) Distanzen vom Clusterzentrum · zum Objekt O₁ und zum Objekt O₂ sind zu quadrieren und anschließend alle vier Werte zu addieren. Somit ist die Vorschrift des Ward-Verfahrens: Fasse jeweils die beiden Cluster zu einem neuen Cluster zusammen, durch deren Verschmelzung die SQS am wenigsten erhöht wird.

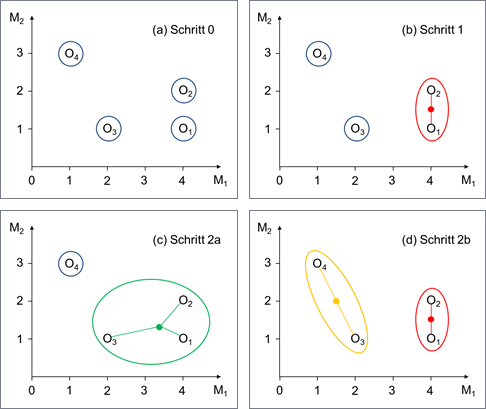Abbildung 1: Beispiel mit zwei Merkmalen

 

Abbildung 2: Streuungsquadratsumme für verschiedene Klassifikationen

 

Veranschaulichung des Algorithmus anhand des Beispiels aus Abbildung 1:

Schritt 0: Ausgangspunkt sind 4 Cluster, die jeweils ein Objekt enthalten (siehe Abbildung 1a).

Schritt 1: Abbildung 2 zeigt die 6 verschiedenen Möglichkeiten, zwei Cluster zu einem neuen zusammen zu fassen. Werden die Cluster {O₁} und {O₂} zu einem fusioniert (siehe Abbildung 1b), so erhöht sich die SQS am wenigsten: die quadrierte Distanz von O₁ zum Clusterzentrum beträgt (4 – 4)² + (1 – 1,5)² = 0,25, die quadrierte Distanz von O₂ zum Clusterzentrum (4 – 4)² + (2 – 1,5)² = 0,25. Insofern ergibt sich eine Streuungsquadratsumme von 0,5, da in den übrigen beiden Clustern nur jeweils ein Objekt enthalten ist.

Schritt 2: Neben den Möglichkeiten zu dem im Schritt zuvor gebildeten Cluster {O₁,O₂} entweder das Cluster {O₃} (siehe Abbildung 1c) oder das Cluster {O₄} (ohne eigene Abbildung) hinzuzufügen, könnten auch die Cluster {O₃} und {O₄} zu einem Cluster vereinigt werden (siehe Abbildung 1d). Letztere führt zur geringsten SQS, so dass sich nach dem zweiten Schritt 2 Cluster mit jeweils 2 Objekten ergeben.

Schritt 3: Die beiden Cluster werden abschließend zu einem fusioniert, das dann alle Objekte enthält.

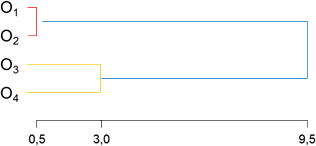
Abbildung 3 veranschaulicht den Fusionsprozess in einem Dendrogramm.

Abbildung 3: Dendrogramm zum Ward-Verfahren

Mögliche Klassifikationen sind somit neben der anfänglichen, in der alle Objekte eigenständige Cluster sind, bzw. der letzten, in der alle Objekte zu einem Cluster gehören, {O₁,O₂}, {O₃} und {O₄} nach Schritt 1 und {O₁,O₂} und {O₃,O₄} nach Schritt 2. Mögliche Kriterien, die zur Auswahl einer Klassifikation verwendet werden können, werden in einem kommenden Beitrag dieser Reihe vorgestellt.

 

Unterschiedliche Skalenniveaus

Das Ward-Verfahren kann sowohl für metrische, ordinale als auch dichotome Variablen eingesetzt werden. Nominale Variablen mit mehr als zwei Ausprägungen können berücksichtigt werden, wenn sie in dichotome Variablen aufgelöst werden. Damit die Anzahl der Ausprägungen nicht Einfluss auf die Bildung der Cluster nimmt, sind die dichotomen Variablen dann entsprechend zu gewichten. Werden gleichzeitig Variablen unterschiedlicher Skalenniveaus herangezogen, sollten die Variablen standardisiert werden, damit nicht ein Merkmal mit einer sehr breiten Skala bestimmend für die Distanz und damit für die Zusammensetzung der Cluster ist.

Beitrag aus planung&analyse 15/2 in der Rubrik „Statistik kompakt“

 

Autoreninformation

Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.

Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.

 

Literatur

Bacher, J.; Pöge, A.; Wenzig, K.: Clusteranalyse. 3. Auflage, 2010, München, S. 285-297.

Backhaus, K.; Erichson, B.; Plinke, W., Weiber, R.: Clusteranalyse. In: Multivariate Analysemethoden. Berlin, Heidelberg: Springer, 13. Auflage, 2011, S. 395-436.

 
<

---

Share