Hauptkomponentenanalyse zur Datenreduktion
Johannes Lüken / Dr. Heiko Schimmelpfennig
Die Hauptkomponentenanalyse wird häufig eingesetzt, um die Menge beobachteter Variablen auf eine geringere Anzahl Faktoren (Hauptkomponenten) so zu reduzieren, dass der Informationsverlust möglichst gering ist. Wesentliche Schritte sind die Bestimmung der Anzahl der Hauptkomponenten und deren Interpretation.
Faktorladungs- bzw. Komponentenmatrix
Zentrales Ergebnis gleich welchen Verfahrens der Faktorenanalyse ist die Faktorladungsmatrix. Sie zeigt die Zusammenhänge zwischen den in die Analyse eingehenden Variablen und den extrahierten Faktoren auf. In Abbildung 1 ist eine Faktorladungsmatrix (Komponentenmatrix) mit allen möglichen Hauptkomponenten für sieben Merkmale aus einer Studie zur Zufriedenehit von Strandurlaubern dargestellt (Schimmelpfennig 2016).
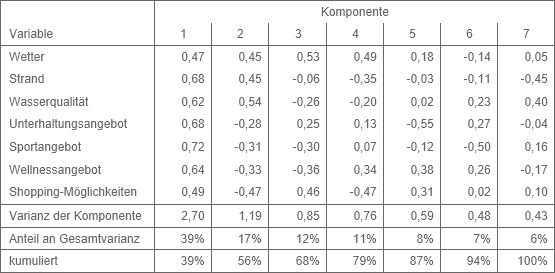Abbildung 1: Beispielhafte Faktorladungsmatrix als Ergebnis einer Hauptkomponentenanalyse
Eine Faktorladung entspricht der Korrelation zwischen einer Variable und einem Faktor. Per Konvention gilt eine Ladung ab 0,5 als hoch. Die quadrierte Faktorladung ist der Anteil der Varianz einer Variablen, der durch einen Faktor erklärt wird. Der durch die Faktoren erklärte Anteil der Varianz einer Variable wird als Kommunalität bezeichnet. Für die Variable Wetter beträgt sie beispielsweise für die ersten beiden Komponenten 0,47² + 0,45² = 0,42. Das Prinzip der Hauptkomponentenanalyse ist es, dass die Kommunalität jeder Variablen bei Berücksichtigung aller Komponenten gleich eins ist. Das heißt ihre gesamte Varianz kann durch die Komponenten erklärt werden.
Bei standardisierten Variablen entspricht die Summe der quadrierten Faktorladungen über alle Variablen der Varianz einer Hauptkomponente. Die Gesamtvarianz ist dann gleich der Anzahl der Variablen, da jede standardisierte Variable eine Varianz von eins besitzt. Der Quotient ergibt somit den Anteil der durch eine Hauptkomponente erklärten Varianz aller Variablen.
Anzahl der Hauptkomponenten
Grundsätzlich besteht ein Trade-off zwischen dem Wunsch nach Datenreduktion und möglichst wenig Informationsverlust. Die Empfehlung von Kaiser (1960) ist ein gängiges Kriterium, an dem sich bei der Entscheidung orientiert wird, wie viele der möglichen Faktoren tatsächlich genutzt werden: Es sind die Hauptkomponenten zu verwenden, deren Varianz größer als eins und damit größer als die einer einzelnen standardisierten Variable ist. In dem Beispiel trifft dies auf die ersten beiden Komponenten zu. Andere Faustregeln geben vor, dass die Hauptkomponenten zusammen zum Beispiel mindestens 2/3 der Gesamtvarianz erklären sollen. Aber auch die Interpretierbarkeit des Ergebnisses darf nicht außer Acht gelassen werden.
Interpretation der Hauptkomponenten
Fast alle Variablen in Abbildung 1 „laden hoch auf“ die erste Hauptkomponente. Sie ist eine Art gewichteter Mittelwert der sieben Merkmale, für die die Zufriedenheit erhoben wurde. Das heißt mithilfe der ersten Hauptkomponente können die Befragten anhand ihrer Gesamtzufriedenheit differenziert werden. Ursache ist das Grundprinzip bei der Bildung der Haupkomponenten, dass jede sequenziell ein Maximum an Varianz erhält. Damit drückt die erste so etwas wie Gesamtbewertung aus, während die übrigen innhaltlich nur noch schwer einzuordnen sind.
Leichter sind Faktoren zu interpretieren, sofern die Faktorladungsmatrix eine Einfachstruktur aufweist. Wenn Faktoren bei einigen Variablen eine hohe und bei den übrigen Variablen eine geringe Ladung haben, können „einfach“ Gruppen von Variablen identifiziert werden, die zusammenhängen. Um eine Faktorladungsmatrix in eine Matrix zu transformieren, die der Einfachstruktur möglichst nahe kommt, gibt es eine Vielzahl an Verfahren. Das gängigste ist die Varimax-Rotation: Die Varianz der quadrierten Ladungen eines Faktors wird maximiert unter der Bedingung, dass die Kommunalitäten gleich bleiben. Für das Beispiel ergibt sich mit zwei Hauptkomponenten die in Abbildung 2 dargestellte Faktorladungsmatrix.
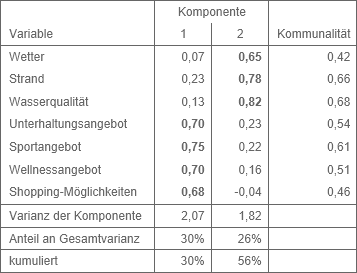
Abbildung 2: Faktorladungsmatrix mit zwei Komponenten nach Anwendung der Varimax-Rotation
Die durch die beiden Komponenten zusammen erklärte Varianz in Höhe von 56% bleibt gleich, sie verteilt sich nur anders auf die Komponenten. Komponente 1 repräsentiert eindeutig die Zufriedenheit mit den sonstigen Aktivitäten in einem Strandurlaub, Komponente 2 die Zufriedenheit mit den Bedingungen für Strandaktivitäten.
Beitrag aus planung&analyse 20/3 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Literatur
Kaiser, H. F.: The Application of Electronic Computers to Factor Analysis. In: Educational and Psychological Measurement, Nr. 1/1960, S. 141-151.
Schimmelpfennig, H: Bekannte, aktuelle und neue Anforderungen an Treiberanalysen. In: Keller, B. et al. (Hrsg.): Marktforschung der Zukunft – Mensch oder Maschine?, Wiesbaden, 2016, S. 231-243.
<
Share
