
Erfolgswirkung von Marken-Touchpoints
Johannes Lüken / Dr. Heiko Schimmelpfennig
Die Beurteilung des wirtschaftlichen Erfolgs von Marketing-Maßnahmen ist immer dann schwierig, wenn Veränderungen monetärer Größen nicht eindeutig einzelnen Maßnahmen zurechenbar sind oder diese erst mit zeitlicher Verzögerung auftreten. Als Ausweg kann zur Erfolgsmessung auf nichtmonetäre, sogenannte vorökonomische Zielgrößen wie Kundenzufriedenheit oder Kundenloyalität zurückgegriffen werden, die nicht direkt beobachtbar (latent) sind (Rese und Herter 2005). Um Ansatzpunkte zu erhalten, wie diese geeignet beeinflusst werden können, kommen häufig Kausalanalysen zum Einsatz – genauer Strukturgleichungsmodelle mit latenten Variablen. Mithilfe dieser Verfahren gelingt es, die entscheidenden Treiber der Zielgrößen zu identifizieren, die Reihenfolge der Treiber hinsichtlich ihrer Bedeutung zu bestimmen und ihr Zusammenspiel untereinander zu durchleuchten.
Strukturgleichungsmodelle zur Beurteilung der Erfolgswirkung von Marken-Touchpoints
Nicht jeder der vielen Punkte, an denen Kunden mit einer Marke in Berührung kommen, ist in gleicher Weise maßgeblich für den Erfolg dieser Marke. Insofern ist die Identifikation der für ausgewählte vorökonomische Zielgrößen relevanten Marken-Touchpoints von großer Bedeutung für das Touchpoint-Management (Esch et al. 2010). Abbildung 1 zeigt beispielhaft ein grundlegendes Strukturgleichungsmodell zur Ermittlung der Wichtigkeit ausgewählter Touchpoints für das Markenimage und die Kundenloyalität. Dieses Modell geht davon aus, dass die positiven bzw. negativen Erfahrungen, die eine Person an diesen Touchpoints mit einer Marke gemacht hat, die einzelnen Imagedimensionen beeinflussen, anhand derer die Marke wahrgenommen wird. Diese wiederum sind maßgeblich für die Kundenloyalität. Zusätzlich dargestellt sind (als Quadrate) die Indikatoren zur Operationalisierung der latenten Variablen. Im Rahmen einer Befragung von Kunden lassen sie sich am einfachsten durch geeignet formulierte und auf einer Rating-Skala zu beurteilende Items erfassen.
Die Ergebnisse der Schätzung des Modells ermöglichen u.a. diese Fragen zu beantworten:
- Welche Marken-Touchpoints sind für die Beurteilung welcher Imagedimensionen relevan
- Welche Marken-Touchpoints sind für die Kundenloyalität am wichtigsten?
Allerdings weisen Daten zur Schätzung derartiger Modelle in der Regel Eigenschaften auf, die es verhindern, dass mithilfe der gängigen Ansätze der Kovarianz Strukturanalyse und des Partial-Least-Squares-Verfahrens (PLS) zur Schätzung von Strukturgleichungsmodellen valide und reliable Ergebnisse erzielt werden können.
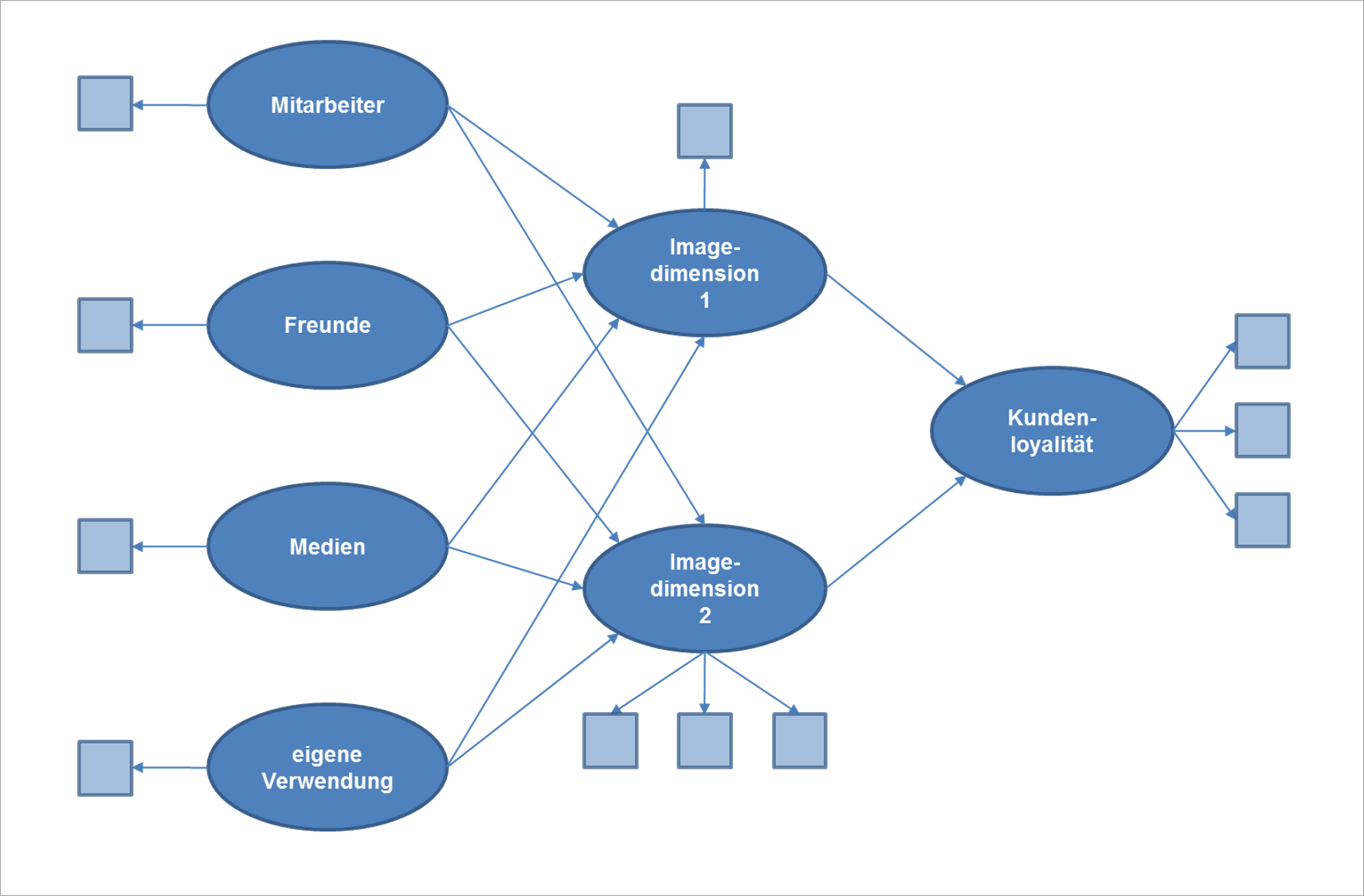
Abbildung 1: Strukturgleichungsmodell zur Analyse der Treiber der Kundenloyalität
Denn ebenso wie in Treiberanalysen der Kundenzufriedenheit die Zufriedenheiten einzelner Aspekte zusammenhängen, korrelieren häufig auch die Erfahrungen mit den einzelnen Touchpoints untereinander. Mit anderen Worten: Einflussvariablen sind von Multikollinearität betroffen. Darüber hinaus enthalten die meisten empirisch erhobenen Datensätze fehlende Werte, deren undifferenzierte Behandlung die Ergebnisse verfälscht. Die damit einhergehenden Probleme werden im Folgenden verdeutlicht und Lösungswege aufgezeigt.
Auswirkungen von Multikollinearität
Das Modell aus Abbildung 1 wurde mittels PLS und Kovarianz Strukturanalyse geschätzt. Abbildung 2 stellt einen Teil der Ergebnisse der PLS-Schätzung dar, die denen der Kovarianz Strukturanalyse sehr ähnlich sind. Sie zeigt die standardisierten Pfadkoeffizienten zur Quantifizierung der Stärke des Einflusses der Erfahrungen mit den Touchpoints auf die Imagedimension 1. Offensichtlich widerspricht dieses Resultat insbesondere der hohen Korrelation zwischen den Äußerungen von Freunden über die Marke und der Imagedimension 1. Insofern ergibt sich ein nur schwer nachvollziehbares und gleichsam verwirrendes Gesamtbild der Einflüsse der untersuchten Touchpoints.
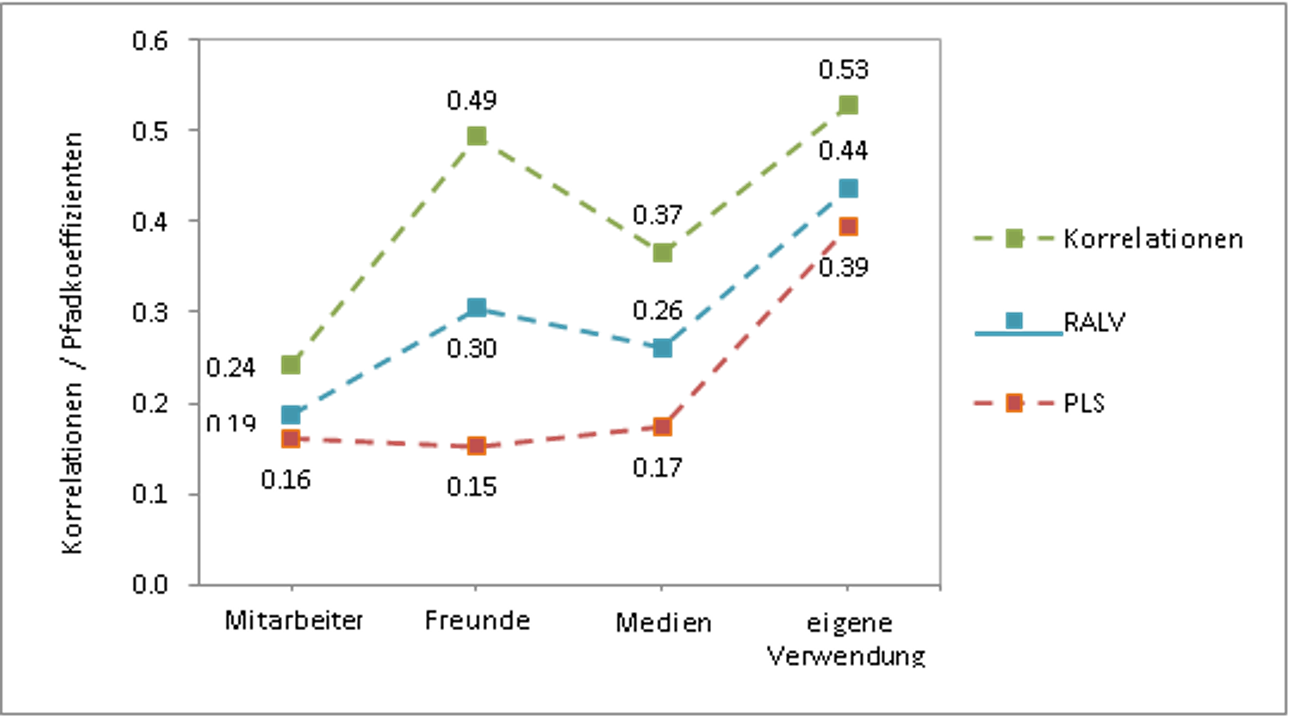
Abbildung 2: Einfluss der Marken-Touchpoints auf Imagedimension 1
Der Grund dafür ist folgender: Die Verfahren berücksichtigen am stärksten den Einfluss der dominierenden Variablen (eigene Verwendung). Der Einfluss der übrigen Variablen, die mit dieser stark korrelieren (im vorliegenden Fall die Gespräche mit Freunden), wird unterdrückt (Suppressionseffekt). Wenn Einflussvariablen einer zu erklärenden Variablen interkorrelieren, ist es prinzipiell gar nicht möglich, dass alle Variablen mit ihrer gesamten Varianz in die Analyse einfließen. Das Bestimmtheitsmaß würde ansonsten das Maximum 1,0 schnell übersteigen. Der Suppressionseffekt kann erfahrungsgemäß sogar soweit führen, dass sich die inhaltliche Aussage umkehrt, d.h. Variablen deren Einflüsse eigentlich positiv sind, einen signifikant negativen Koeffizienten erhalten. Insofern sind die Pfadkoeffizienten stark interkorrelierender Einflussvariablen nicht mehr vergleichbar und Fehlentscheidungen folglich vorprogrammiert.
Orthogonalisierung zur Lösung des Multikollinearitätsproblems
Das Problem der Multikollinearität wird in der Kovarianz Strukturanalyse weitgehend ignoriert (Grewal et al. 2004) bzw. in PLS nicht zufriedenstellend gelöst (Temme et al. 2010). In Regressionsanalysen ist die Vorschaltung von Faktorenanalysen eine anerkannte Praxis (Hauptkomponenten-Regression). Im Allgemeinen wird dabei im Sinne der originären Aufgabenstellung der Faktorenanalyse auf eine reduzierte Anzahl voneinander unabhängiger Dimensionen zurückgegriffen und deren Einflussstärken bestimmt. Allerdings geht damit nicht nur ein Teil der erklärten Varianz der abhängigen Variablen verloren. Darüber hinaus würde dieses Vorgehen innerhalb der Strukturgleichungsmodellierung eine Veränderung des Modells bedeuten, so dass die Wirkung der ursprünglichen erklärenden Variablen z.B. der einzelnen Touchpoints nicht bestimmt wird.
Vielmehr ist es notwendig, die Einflüsse der Treiber klar voneinander zu trennen. Das wird erreicht durch eine besondere Form der Orthogonalisierung: Es werden alle resultierenden Hauptkomponenten einer vollständigen Faktorenlösung zur Abbildung der Originalvariablen genutzt. Dieses Vorgehen stellt eine stringente Fortsetzung der Hauptkomponenten-Regression dar. Auf diese Weise wird zu jeder Einflussvariable eine (neue) latente Variable extrahiert, die ihren einzigartigen inhaltlichen Kern repräsentiert. Überschneidungen mit den übrigen in die Hauptkomponentenanalyse eingehenden Variablen und damit Multikollinearität werden ausgeschlossen. Der Anteil der durch die Originalvariablen erklärten Varianz der abhängigen Variablen bleibt somit vollständig erhalten.
Voraussetzung für eine erfolgreiche Orthogonalisierung ist, dass jede Hauptkomponente genügend stark mit ihrer entsprechenden einfließenden Variablen übereinstimmt. Eine Korrelation von 0,80 zwischen der Variable und ihrer zugehörigen Hauptkomponente kann als sehr gut angesehen werden und lässt sich zumeist realisieren. Eine Korrelation von 0,70 ist ausreichend und wird fast immer erreicht.
Mit dem Analyse-Tool RALV (Relationships Among Latent Variables) steht eine Alternative zu den herkömmlichen Ansätzen zur Schätzung von Strukturgleichungsmodellen zur Verfügung, das es ermöglicht, die Orthogonalisierung bei der Schätzung eines vollständigen Strukturgleichungsmodells mit latenten Variablen zu berücksichtigen. Die beschriebene Form der Orthogonalisierung wurde dazu in einen Algorithmus integriert, der sich an dem Vorgehen von PLS orientiert und folgende Schritte umfasst:
- Definition von einem oder mehreren Sets von Variablen, in denen jeweils diejenigen latenten Variablen zusammengefasst werden, die eine endogene Variable beeinflussen und voneinander unabhängig in die Analyse eingehen solle
- Bestimmung konkreter Werte der latenten Variablen für alle Fälle der Stichprobe
- Berechnung neuer Fallwerte für jede Variable innerhalb eines der definierten Sets durch Orthogonalisierung
- Schätzung der Pfadkoeffizienten durch multiple Regressionen auf Basis der bestimmten Fallwerte, in denen jeweils eine latente Variable die zu erklärende Variable und alle ihre unmittelbaren Vorgänger im Strukturgleichungsmodell ihre Einflussvariablen sin
Unter Berücksichtigung der Orthogonalisierung der Erfahrungen mit den Touchpoints resultieren die mit RALV geschätzten ebenfalls in Abbildung 2 dargestellten Koeffizienten. Offensichtlich wird die Suppression des Einflusses der Gespräche mit Freunden verhindert, so dass sich die Einflussstärken der Touchpoints nunmehr deutlich voneinander unterscheiden und die Reihenfolge der Höhe der Pfadkoeffizienten der Reihenfolge der Korrelationen entspricht.
Die Orthogonalisierung ist sowohl möglich für Variablen, die ausschließlich Einflussvariablen sind, als auch für Variablen, die gleichzeitig beeinflusste Variablen sind. D.h. im Strukturgleichungsmodell in Abbildung 1 können auch interkorrelierende Imagedimensionen orthogonalisiert und damit jeweils ihr eigenständiger Einfluss auf die Kundenloyalität bestimmt werden. Der Algorithmus gewährleistet, dass sie mit denselben Fallwerten in die Schätzung der Pfadkoeffizienten eingehen – gleichgültig ob sie als Einflussvariable oder zu erklärende Variable berücksichtigt werden. Insofern ist trotz Orthogonalisierung auch die Berechnung totaler Effekte möglich.
Wird mit den Imagedimensionen 1 und 2 ein zweites Set von zu orthogonalisierenden Variablen definiert, ergeben sich die in Abbildung 3 dargestellten direkten Effekte der Touchpoints auf die Imagedimensionen sowie die totalen Effekte der Touchpoints auf die Kundenloyalität.
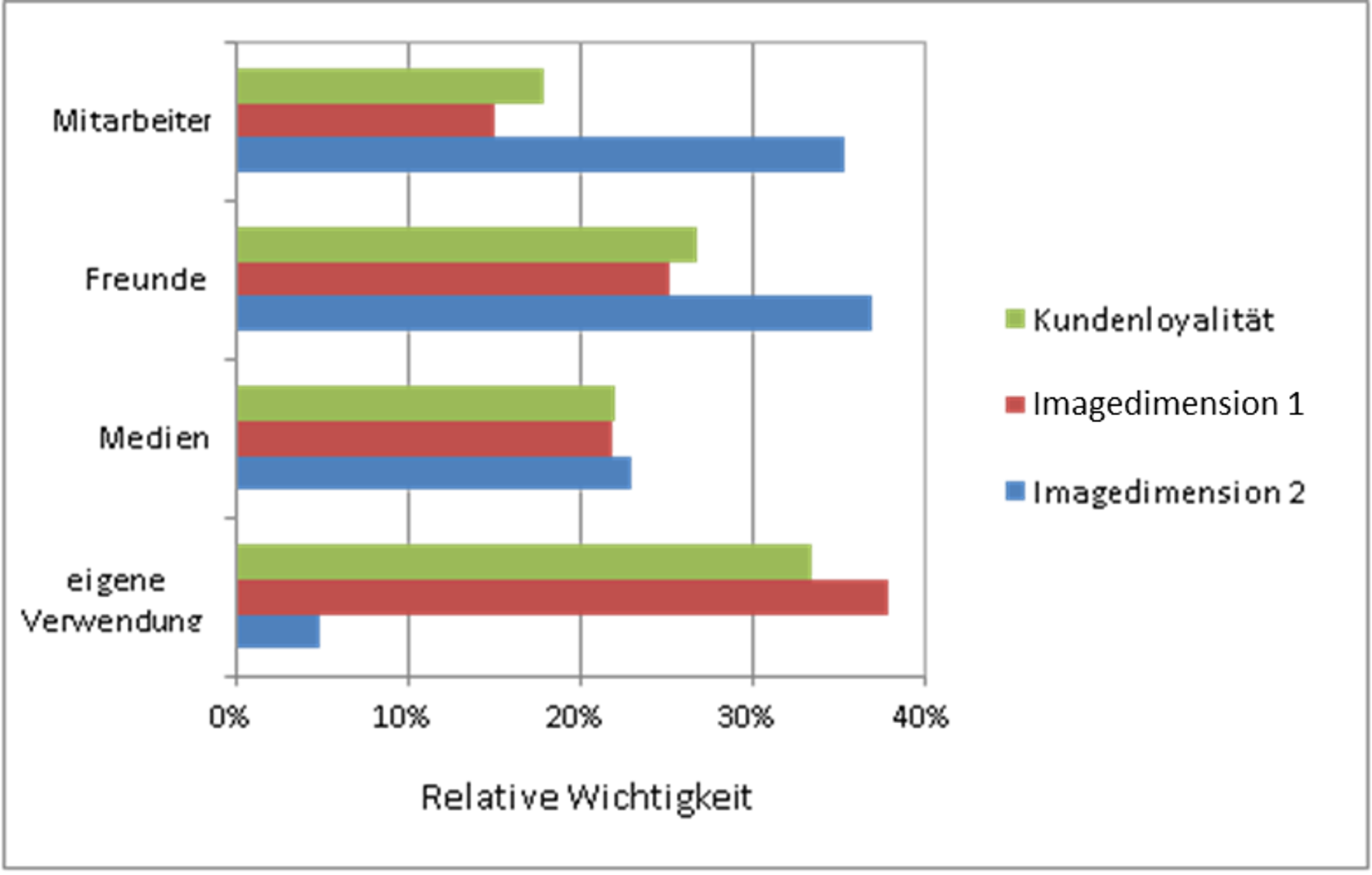
Abbildung 3: Wichtigkeit der Marken-Touchpoints für Kundenloyalität und Imagedimensionen
Offensichtlich sind die Erfahrungen aufgrund der eigenen Verwendung der Marke sowohl für die Dimension 1 als auch für die Kundenloyalität am bedeutendsten, während Dimension 2 insbesondere durch den Kontakt mit Mitarbeitern sowie Freunden beeinflusst wird.
Systematische Mean Substitution zur Lösung des Missing Values Problems
In kaum einem empirisch gewonnenen Datensatz kann man von lückenlosen Angaben ausgehen. Sowohl einfachere (Listwise Deletion und Mean Substituion) als auch komplexere Ansätze (EM- Algorithmus und Multiple Imputation) zur Behandlung von Missing Values setzen Zufälligkeit des Auftretens fehlender Werte voraus. D.h. ihr Auftreten soll insbesondere unabhängig von Ausprägungen anderer Variablen sein.
Das Ersetzen von Missing Values durch Mittelwerte kann aber auch sinnvoll sein, wenn sich fehlende Werte nicht zufällig verteilen und die dahinter liegende Systematik genutzt wird. Missing Values stellen bei einer solchen Betrachtung kein Problem dar, sondern liefern verwertbare Information.
Wenn ein Befragter zu einem vorgelegten Item keine Angabe macht, kann gerade in Treiberanalysen bei entsprechender Fragestellung davon ausgegangen werden, dass dieses Item (dieser Treiber) für ihn keine Bedeutung besitzt. Ersetzt man die fehlenden Angaben durch den Mittelwert dieses Items auf Basis aller Fälle, die geantwortet haben, reduziert sich aufgrund der verringerten Varianz ein zu diesem Treiber gehörender Koeffizient im Vergleich zu dem Wert, der nur auf Basis der Fälle geschätzt wird, die eine Angabe gemacht haben.
Inhaltlich kann das im Sinne der Aufgabenstellung sein: Ein hoher Zusammenhang mit einer ab- hängigen Größe kommt eher dann zustande, wenn das Item für viele Befragte relevant ist. Gibt es nur wenige Befragte, die zu diesem Punkt etwas zu sagen haben, ist der Einfluss bezogen auf die Gesamtgruppe geringer – auch wenn für diese Befragten allein ein hoher Einfluss besteht. Aspekte, die nur einen Teil der Befragten betreffen, verlieren somit insgesamt an Einflussstärke. Im Gegensatz zur Mittelwertersetzung bei zufälligem Fehlen stellen entsprechende Veränderungen der Koeffizienten somit keine Verzerrungen dar, sondern verbessern die Güte der Schätzung.
Innerhalb der Marken-Touchpoint-Analyse ist es insofern gerechtfertigt, fehlende Werte bei Indikatoren der Erfahrungen mit den Touchpoints durch den jeweiligen Mittelwert zu ersetzen, wenn im Modell deren Einflüsse auf die Imagedimensionen untersucht werden und mit dem Fehlen der Antwort zum Ausdruck gebracht wird, dass dieser Touchpoint für die Befragten keine Bedeutung besitzt, weil sie ihn nicht nutzen.
Allerdings sollte ein Grenzwert definiert werden, der übermäßig lückenhafte Datensätze ausfiltert. Anforderungen an die Anzahl der vorhandenen Antworten je Fall für das gesamte Modell zu definieren, ist jedoch problematisch. Dies wird besonders deutlich, wenn das Modell um eine weitere Ebene unterhalb der Touchpoints erweitert wird, auf der einzelne Attribute des jeweiligen Touchpoints bewertet werden, um unmittelbare Ansatzpunkte für Veränderungen aufzudecken.
Abbildung 4 zeigt die Erweiterung beispielhaft für den Kontakt mit den Mitarbeitern des für die Marke verantwortlichen Unternehmens.
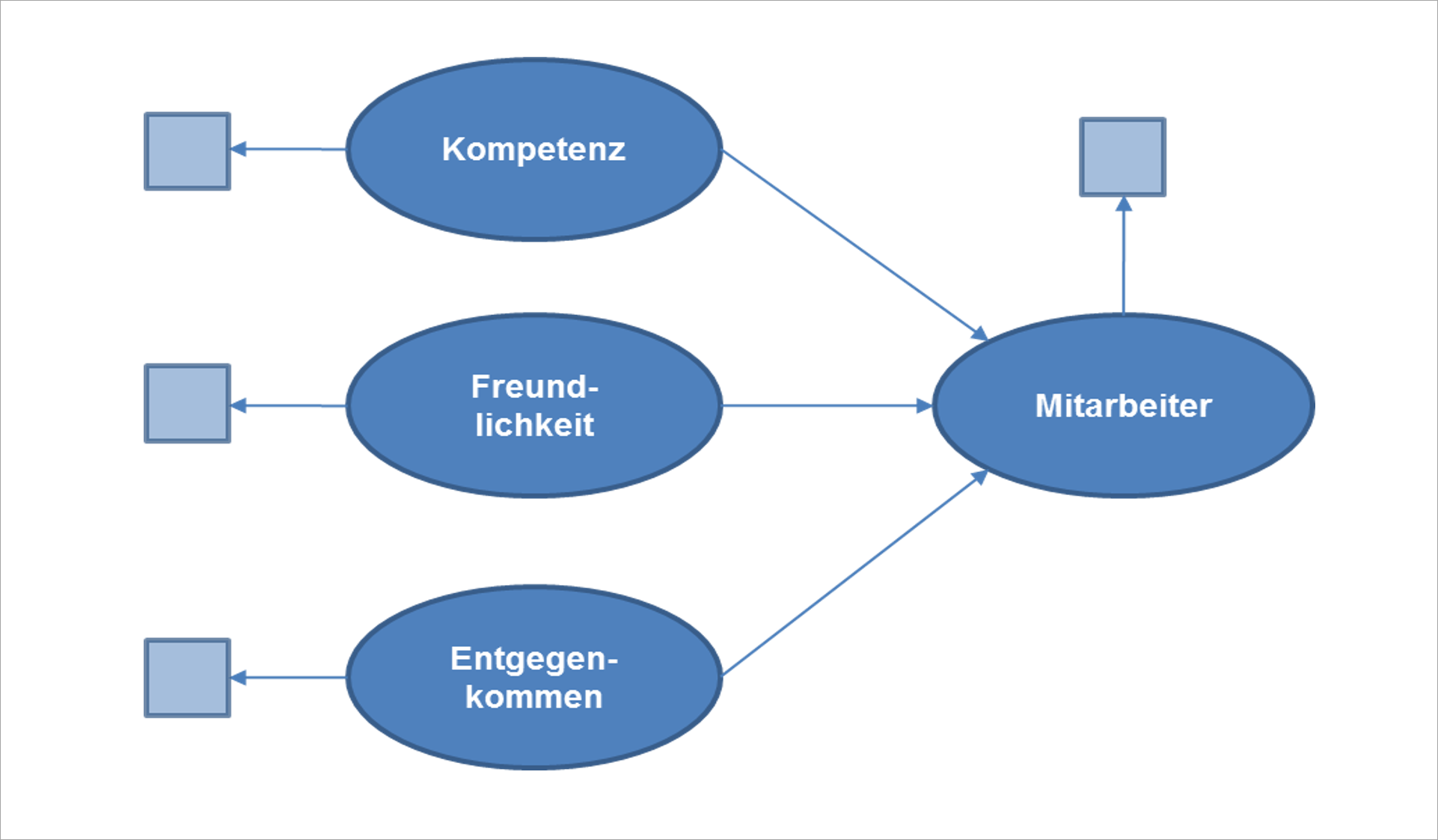
Abbildung 4: Ausschnitt aus dem um Beurteilungen von Attributen der Touchpoints erweiterten Strukturgleichungsmodell aus Abbildung 1
Hat jemand beispielsweise alle Items mit Ausnahme der vier zu den Erfahrungen mit Mitarbeitern beantwortet, weil er solche nicht gemacht hat, werden bei undifferenzierter Vorgehensweise alle vier fehlenden Werte durch den Mittelwert ersetzt. Somit verringert sich nicht nur der Einfluss dieses Touchpoints auf die Imagedimensionen, sondern auch der der Attribute auf den Touchpoint. Gäbe es kaum Fälle, die diese Items beantwortet haben, ergäbe sich infolge der Analyse, dass alle Attribute für den Touchpoint unbedeutend sind. Auch ohne dieses Ergebnis zu quantifizieren, wird an dem Beispiel aus Abbildung 4 deutlich, wie wenig plausibel es wäre.
Wird dagegen wie in RALV die Anforderung an die Anzahl vorhandener Werte für jedes Teilmodell,
d.h. jede durchzuführende multiple Regressionsanalyse, einzeln berücksichtigt, entfällt für den beschriebenen Fall eine Ersetzung der Missing Values durch Mittelwerte bei der Beurteilung der Attribute. D.h. der Fall bleibt zur Schätzung der Einflüsse auf die Erfahrungen mit Mitarbeitern unberücksichtigt. Nur auf der Ebene der Gesamtbeurteilungen der Touchpoints erfolgt wunschgemäß die Ersetzung der fehlenden Werte.
Fazit
Multikollinearität und fehlende Werte verschlechtern erheblich die Ergebnisse von Treiberanalysen, wie z.B. im Rahmen einer Marken-Touchpoint-Analyse zur Bestimmung der für ausgewählte Zielgrößen relevanten Touchpoints.
Durch Orthogonalisierung werden Interkorrelationen zwischen Einflussvariablen eliminiert und deren einzigartigen voneinander unabhängigen Kernaussagen zur Schätzung der Pfadkoeffizienten in einem Strukturgleichungsmodell verwendet. Diese werden vergleichbar und deutlich stabiler im Hinblick auf Veränderungen in der Modellierung.
Mit fehlenden Werten ist in einzelnen Teilmodellen eines Strukturgleichungsmodells differenziert umzugehen. Ein Ersetzen fehlender Werte durch Mittelwerte ist immer dann anwendbar, wenn das Nichtvorhandensein eines Wertes im Sinne geringer Bedeutung interpretierbar ist. Voraussetzungen dafür sind entsprechende Fragestellungen und Antwortkategorien.
Veröffentlichung mit Genehmigung des Deutschen Fachverlages GmbH, planung & analyse, Mainzer Landstrasse 251, 60326 Frankfurt am Main, Telefon 069-7595-2019, Fax 069-7595-2017, redaktion@planung-analyse.de, www.planung-analyse.de
Beitrag aus Heft 4/2011, S. 61-64
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Esch, Franz-Rudolf; Brunner, Christian; Gawlowski, Dominika; Knörle, Christian; Kriege, Kai Harald: Customer Touchpoints marken- und kundenspezifisch managen. In: Marketing Review St. Gallen, Jg. 27/2010, Nr. 2, S. 8-13.
Grewal, Rajdeep; Cote, Joseph A.; Baumgartner, Hans: Multicollinearity and Measurement Error in Structural Equation Models. Implications for Theory Testing. In: Marketing Science, Vol. 23/2004, No. 4, S. 519-529.
Rese, Mario; Herter, Valerie: Erfolgsbeurteilung und -kontrolle im Marketing. In: WISU Das Wirtschaftsstudium, Jg. 34/2005, Nr. 8/9, S. 1010-1011.
Temme, Dirk; Kreis, Henning; Hildebrandt, Lutz: A Comparison of Current PLS Path Modeling Software: Features, Ease-of-Use, and Performance. In: Esposito Vinzi, Vincenzo; Chin, Wynne W.; Henseler, Jörg; Wang, Huiwen (Hrsg.): Handbook of Partial Least Squares. Concepts, Methods and Applications, Berlin: Springer 2010, S. 737-756.
Und mit diesem Onlinetool können Sie orthognalisiertE Kausalanalysen durchführen
<







