
Entscheidungsbäume – Algorithmen im Überblick
Johannes Lüken / Dr. Heiko Schimmelpfennig
Entscheidungsbäume können zur Segmentierung und Prognose eingesetzt werden. Sie teilen einen Datensatz in einer baumartigen hierarchischen Struktur in immer kleiner und hinsichtlich einer abhängigen Variable immer homogener werdende Teilgruppen (Knoten) auf. An jeder Verzweigung wird eine der unabhängigen Variablen (die Trennungsvariable) genutzt, um die Fälle aufzuteilen. Den Endknoten wird schließlich eine Ausprägung der abhängigen Variable zugeordnet. Dies ist je nach Skalenniveau ihr Modal- oder Mittelwert für die Fälle eines Endknotens. Aus dem Baum lassen sich unmittelbar Regeln zur Prognose der abhängigen Variable für neue Fälle ableiten. Wichtige Algorithmen zur Induktion von Entscheidungsbäumen sind ID3 (1986) beziehungsweise sein Nachfolger C4.5 (1993), CHAID (1980), CART (1984) und CTree (2006), die sich anhand verschiedener Kriterien differenzieren lassen.
Induktion des Baumes
Der offensichtlichste Unterschied ist die Anzahl möglicher Verzweigungen, die von einem Knoten ausgehen. Eine Gruppe von Algorithmen lässt nur zwei Verzweigungen zu, die andere maximal so viele wie die Trennungsvariable Kategorien aufweist. Zur Bestimmung der Trennungsvariable nutzen die Algorithmen verschiedene Kriterien. Diese können im Wesentlichen unterteilt werden in statistische Tests einerseits und Informationsmaße andererseits, die die „Unreinheit“ der Knoten messen. Ein Knoten wird als „rein“ bezeichnet, wenn alle seine Fälle dieselbe Ausprägung der abhängigen Variable aufweisen. Statistische Tests dienen gleichzeitig als Kriterium, um das Verzweigen zu stoppen. Informationsmaße treffen dagegen keine Aussage, ob sich durch eine weitere Verzweigung das Maß signifikant verbessert. Daher wird ein Baum größer und er neigt zu einem Overfitting an die vorliegenden Daten. Um den Baum sinnvoll zur Prognose anderer Fälle nutzen zu können, ist er durch ein „Zurückschneiden“ allgemeingültiger zu machen. Zum Beispiel wird für jeden Knoten oberhalb der Endknoten anhand eines zweiten Validierungsdatensatzes überprüft, ob der Baum unterhalb des Knotens notwendig ist, um die Prognosegüte bedeutend zu erhöhen. Anhand der Anzahl möglicher Verzweigungen und dem Trennungskriterium lassen sich die vier Algorithmen eindeutig klassifizieren und selbst in einem Baum wie in der Abbildung darstellen.
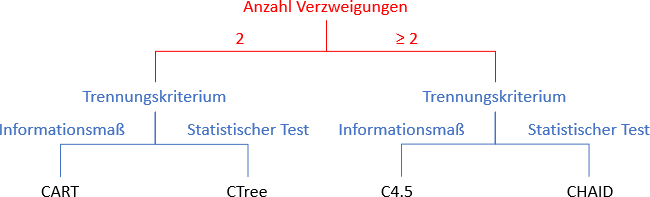
Abbildung: Klassifikation von Algorithmen zur Induktion von Entscheidungsbäumen
Unverzerrtheit der Auswahl der Trennungsvariable
Algorithmen, die ein Informationsmaß nutzen, tendieren bei der Auswahl der Trennungsvariable dazu, Variablen mit vielen Kategorien zu bevorzugen. Auch CHAID zeigt hierbei im Gegensatz zu CTree eine Abhängigkeit von der Anzahl der Kategorien.
Gewichtung der unabhängigen Variablen
C4.5 und CART ermöglichen eine Gewichtung der Variablen, um die Auswahl bewusst zu beeinflussen. Mit dieser Gewichtung kann beispielsweise berücksichtigt werden, dass einige Variablen im Hinblick auf die Prognose neuer Fälle schwieriger zu erheben sind als andere. Die Idee ist, der Auswahl der Variable nicht die absolute Verbesserung des Informationsmaßes zugrunde zu legen, sondern sie in Relation zu den „Kosten“ zu setzen und quasi eine Verbesserung „je Euro“ zu bestimmen.
Skalenniveaus der Variablen
Während C4.5 nur bei einer kategorialen abhängigen Variable eingesetzt werden kann, gibt es im Hinblick auf das Skalenniveau der abhängigen und unabhängigen Variablen bei den anderen Algorithmen keine Einschränkung. CHAID und C4.5 erfordern jedoch eine Kategorisierung metrischer unabhängiger Variable vor Beginn der Induktion des Baumes.

Fehlende Werte bei unabhängigen Variablen
Bei CHAID stellen fehlende Werte einer Variable eine eigene Kategorie dar. CTree, CART und C4.5 schließen fehlende Werte bei der Berechnung der Trennungskriterien aus. Für die Prognose nutzen CTree und CART dann Surrogate, das heißt Variablen die der eigentlichen Trennungsvariable an dieser Stelle des Baumes im Hinblick auf die Aufteilung am ähnlichsten sind. C4.5 kann einen Fall gemäß der Verteilung der eigentlichen Trennungsvariable in dem Datensatz auf die Knoten aufteilen. Grundsätzlich ist es auch möglich, fehlende Werte vorab zu ersetzen: entweder durch Imputation oder bei kategorialen Variablen durch einen numerischen Wert wie die beliebte „99“, so dass dieser wie in CHAID als eigene Kategorie behandelt wird.
Auswahl des Algorithmus
Kommen vor dem Hintergrund dieser Kriterien mehrere Algorithmen infrage, kann der „richtige“ Algorithmus anhand von Prognosegütemaßen wie der Trefferquote ausgewählt werden. Dazu wird der auf Basis eines Trainingsdatensatzes erstellte Baum genutzt, um die Fälle eines Validierungsdatensatzes zu prognostizieren. Auch die Komplexität eines Baumes und damit verbunden die Einfachheit der Interpretierbarkeit kann mit ins Kalkül gezogen werden.
Beitrag aus planung&analyse 18/2 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Hothorn, T.; Hornik, K.; Zeileis; A.: Unbiased Recursive Partitioning: A Conditional Inference Framework. In: Journal of Computational and Graphical Statistics, Nr. 3/2006, S. 651-674.
Rokach, L.; Maimon, O.: Decision Trees. In: Maimon, O.; Rokach, L. (Hrsg.): Data Mining and Knowledge Discovery Handbook, New York, 2005, S. 165-192.
<





