Einführung in Signifikanztests
Johannes Lüken / Dr. Heiko Schimmelpfennig
Signifikanztests untersuchen, inwieweit die auf Grundlage einer Stichprobe erzielten Ergebnisse auch in der dahinter liegenden Grundgesamtheit gelten. Da die wahren Werte von Parametern der Grundgesamtheit wie Mittelwert, Anteil, Korrelations- oder Regressionskoeffizient nicht bekannt sind, werden hypothetische Werte angenommen und überprüft, ob diese mit den Werten in der Stichprobe im Widerspruch stehen.
Beispiel
Es soll untersucht werden, ob sich nach dem erstmaligen Verbrauch eines Produktes die Kaufbereitschaft für das Produkt verändert. Dazu wird vorher und nachher dieselbe zufällig ausgewählte Stichprobe der Zielgruppe befragt. Nimmt man an, dass sich im Durchschnitt die Kaufbereitschaft aller Personen der Zielgruppe nicht verändert, so würde als Hypothese folgen: „Die wahren Mittelwerte der Kaufbereitschaft sind vor und nach dem Verbrauch gleich“.
Intuitives Vorgehen
Man berechnet für jeden Befragten der Stichprobe die Differenz zwischen seiner Kaufbereitschaft vor und nach dem Verbrauch und bildet dann den Mittelwert über diese Differenzen. Gegen die aufgestellte Hypothese würde sprechen, wenn der Mittelwert deutlich von null abweicht. Mithilfe eines Signifikanztests wird nun präzisiert, ab wann Abweichungen des Mittelwertes von null in der Stichprobe deutlich oder bloß zufällig sind.
Stichprobenverteilung
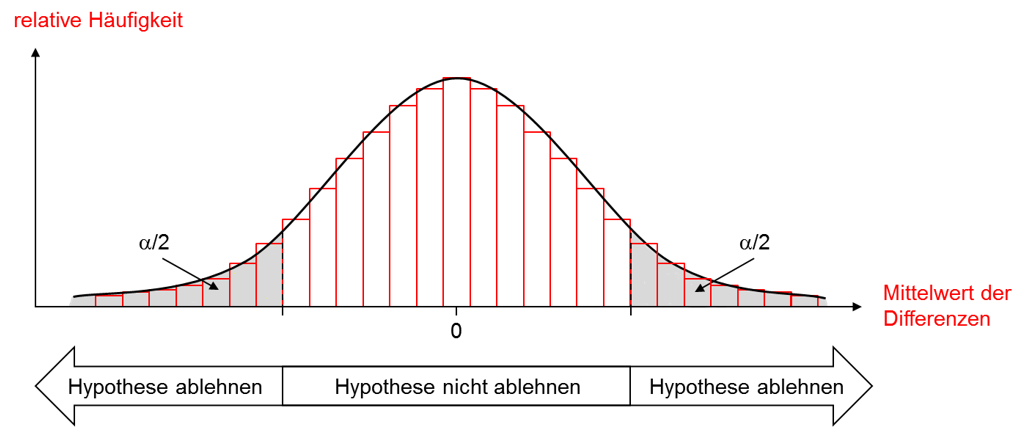
Eine vorliegende Stichprobe ist nur eine von vielen möglichen. Geht man von der Richtigkeit der Hypothese aus, das heißt in der Grundgesamtheit aller Personen der Zielgruppe ist der Mittelwert der Differenzen gleich null, und würde sämtliche Stichproben des gleichen Umfangs ziehen, so verteilen sich deren Mittelwerte wie in dem roten Histogramm der Abbildung skizziert. Für sehr viele Stichproben ergibt sich ein Mittelwert, der in der Nähe von null liegt, für sehr wenige Stichproben ein Mittelwert, der sehr weit davon entfernt ist.
Aber auch ohne alle möglichen Stichproben dieses Umfangs gezogen zu haben, lässt sich unter der Bedingung, dass die Hypothese richtig ist, die für einen Signifikanztest maßgebliche Verteilung der Teststatistik ermitteln. Im beschriebenen Beispiel ist der Mittelwert der Differenzen für Stichproben mit einem Umfang größer als 30 annähernd normalverteilt, wie die schwarze Kurve in der Abbildung veranschaulicht.
Signifikanzniveau
Ein sehr großer Mittelwert der Differenzen in einer Stichprobe kann in dem Beispiel zwei Gründe haben: Entweder ist in der Grundgesamtheit der Mittelwert tatsächlich nicht null, oder der Mittelwert von null ist richtig, jedoch hat man eine „ungünstige“ Stichprobe erwischt. Im ersten Fall wird mit Ablehnung der Hypothese die richtige Entscheidung getroffen, im zweiten Fall jedoch eine falsche (Fehler 1. Art).
Da der Mittelwert der Differenzen sowohl positiv als auch negativ sein kann, ist im Hinblick auf die Entscheidung über die Hypothese ein Bereich für positive wie ein Bereich für negative Mittelwerte festzulegen. Diese beiden Bereiche sollen alle diejenigen Mittelwerte umfassen, für die die Hypothese abgelehnt wird, weil sie zu weit von null entfernt sind. In der Abbildung sind diese grau unterlegt. Die Wahrscheinlichkeit des Fehlers 1. Art ist damit unter Annahme der Richtigkeit der Hypothese gleich der Wahrscheinlichkeit, eine Stichprobe zu ziehen, deren Mittelwert der Differenzen in einen dieser beiden Bereiche fällt.
Damit die Wahrscheinlichkeit dieses Fehlers sehr gering ist, könnte man die Bereiche sehr schmal halten. Ist die Hypothese aber tatsächlich falsch, wird dies dann leicht nicht mehr erkannt, und man macht ebenfalls einen Fehler (Fehler 2. Art). Die Wahrscheinlichkeit beider Fehler kann somit nicht gleichzeitig minimiert werden. Insofern ist es üblich, die Wahrscheinlichkeit für den Fehler 1. Art, die gerade noch akzeptiert wird – das Signifikanzniveau a – vorzugeben und einen Test zu verwenden, bei dem die Wahrscheinlichkeit für den Fehler 2. Art möglichst klein wird. Durch die Vorgabe von a können mithilfe von Tabellen der ermittelten Verteilung die Grenzen bestimmt werden, innerhalb derer Abweichungen der Mittelwerte der Differenzen von null noch zufällig sind und außerhalb derer sie zu groß sind, um die Hypothese „Die wahren Mittelwerte sind vor und nach dem Verbrauch gleich“ beizubehalten.
Entscheidung anhand des p-Wertes
Mit dem Einsatz von Statistik-Software erübrigt sich eine Bestimmung der Bereiche, um über eine Hypothese zu entscheiden. Die Software weist mit dem p-Wert die Wahrscheinlichkeit aus, unter der Annahme der Richtigkeit der Hypothese in diesem Beispiel einen Mittelwert der Differenzen (allgemein: eine Teststatistik) zu erhalten, der vom Betrag genauso groß wie oder größer als der in der vorliegenden Stichprobe beobachtete Mittelwert ist. Damit gibt p die konkrete Wahrscheinlichkeit für den Fehler 1. Art an. Eine Entscheidung über die Hypothese kann dann unmittelbar auf der Grundlage des p-Wertes getroffen werden.
Ist die Wahrscheinlichkeit p, mit der Ablehnung der Hypothese einen Fehler zu begehen, kleiner als die maximal akzeptierte Fehler-Wahrscheinlichkeit a, wird die Hypothese folglich abgelehnt. Entsprechend der Höhe von p kann dann differenziert werden, ob ein Ergebnis schwach signifikant (p £ 0.1), signifikant (p £ 0.05) oder hoch signifikant (p £ 0.01) ist.
Ist zum Beispiel p = 0.03, so ist die Veränderung der Kaufbereitschaft signifikant, das heißt in der Stichprobe so hoch, dass voraussichtlich auch in der Grundgesamtheit ein Unterschied vorliegt – ohne aber eine Aussage über dessen Höhe zu machen. Dazu wäre es nötig, eine andere Hypothese wie beispielsweise „Der wahre Mittelwert der Kaufwahrscheinlichkeit ist nach dem Verbrauch um mindestens 10 Prozentpunkte höher als vor dem Verbrauch“ zu testen.
Beitrag aus planung&analyse 12/5 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Bleymüller, J.: Statistik für Wirtschaftswissenschaftler, 16. Auflage, München, 2012.
Eckey, H.-F.; Türck, M.: Statistische Signifikanz (p-Wert). In: Wirtschaftswissenschaftliches Studium, Jg. 35/2006, Nr. 7, S. 415-418.
Siegel, S.: Nichtparametrische statistische Methoden, 5. Auflage, Eschborn, 2001.