Einführung in Kausalanalysen

Johannes Lüken / Dr. Heiko Schimmelpfennig

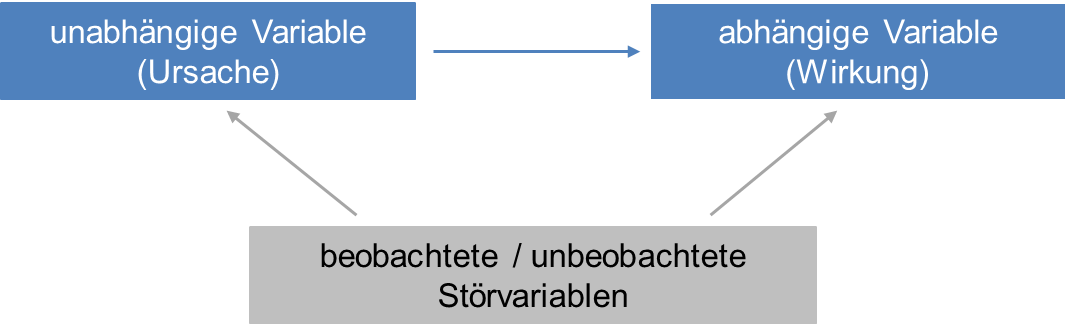
Kausale Zusammenhänge beschreiben Beziehungen zwischen Variablen in Form von Wenn-dann- bzw. Je-desto-Sätzen. Ein typisches Beispiel ist der Zusammenhang zwischen der Kundenzufriedenheit und einem ihrer Treiber wie „Wenn die wahrgenommene Produktqualität steigt, dann erhöht sich die Kundenzufriedenheit“. Die Wenn- oder Je-Komponente enthält die Ursache bzw. unabhängige Variable, die Dann- oder Desto-Komponente die Wirkung bzw. abhängige Variable.

Mit Kausalanalysen werden Vermutungen über kausale Zusammenhänge getestet. Auf diese Weise werden beispielsweise aus der Vielzahl an möglichen Treibern diejenigen bestimmt, die die Kundenzufriedenheit tatsächlich beeinflussen. Dazu können verschiedene Methoden eingesetzt werden, die für die Prüfung der Anforderungen an einen kausalen Zusammenhang unterschiedlich gut geeignet sind.

 

Anforderungen an einen kausalen Zusammenhang

Von einem kausalen Zusammenhang zwischen einer unabhängigen und einer abhängigen Variable kann man ausgehen, wenn

1. zwischen der unabhängigen Variable und der abhängigen Variable ein statistischer Zusammenhang besteht,
2. die Veränderung der unabhängigen Variable der der abhängigen Variable zeitlich vorausgeht, und
3. alternative Erklärungen für den statistischen Zusammenhang ausgeschlossen werden können.

Bezogen auf das Eingangsbeispiel

1. müssen Produktqualität und Zufriedenheit miteinander korrelieren,
2. muss sich die Produktqualität verändert haben, bevor sich die Zufriedenheit verändert, und
3. dürfen Veränderungen von Produktqualität und Zufriedenheit nicht auf andere (dritte) Variablen zurückzuführen sein,

damit ein kausaler Zusammenhang zwischen Produktqualität und Kundenzufriedenheit bestätigt wird.

Überprüfung mittels randomisierten Experimenten

Als ideal für den Test eines kausalen Zusammenhangs gilt das randomisierte Experiment. Die Befragten werden zufällig in so viele Gruppen aufgeteilt wie Ausprägungen der unabhängigen Variable untersucht werden sollen – im einfachsten Fall zwei. Jede andere Variable weist dann bei einer großen Stichprobe in den Gruppen abgesehen von Zufallsschwankungen die gleiche Verteilung auf. Anschließend werden die Ausprägungen der unabhängigen Variable zufällig den Gruppen zugewiesen. Beispielsweise werden zur Überprüfung des Einflusses einer Werbung auf die Kaufbereitschaft die Befragten zufällig in zwei Gruppen aufgeteilt, so dass sie bezüglich der Kaufbereitschaft aber auch anderer Variablen wie Werbe- oder Produktinvolvement gleich sind. Der einen Gruppe wird ein Werbespot gezeigt und einer zweiten (Kontroll-)Gruppe nicht. Unterschiede im Mittel zwischen den Gruppen in der abhängigen Variable (Kaufbereitschaft) können dann eindeutig auf die unabhängige Variable (Werbespot gesehen oder nicht) zurückgeführt werden, da sich die Gruppen in den Variablen vor dem Anschauen des Spots nicht unterschieden haben. Damit lässt sich der durchschnittliche kausale Effekt durch einen Vergleich der Mittelwerte der abhängigen Variable zwischen den Gruppen oder bei vielen Ausprägungen der unabhängigen Variable durch die Korrelation der Werte der unabhängigen und der abhängigen Variable bestimmen. Zudem stellt ein experimentelles Design die zeitliche Asymmetrie von Ursache und Wirkung sicher.

 

Überprüfung bei nicht-experimentellen Designs

In nicht-experimentellen Designs werden Ausprägungen der unabhängigen Variable bei den Befragten nicht künstlich herbeigeführt, sondern liegen bei ihnen bereits vor. Insofern ist die Einteilung in Gruppen mit jeweils gleichen Ausprägungen der unabhängigen Variable vorgegeben. Aller Voraussicht nach werden sich aber auch die Werte anderer Variablen zwischen den Gruppen unterscheiden. Beispielsweise könnten in einer Gruppe, die die Produktqualität als gut beurteilt, sowohl die Kundenzufriedenheit als auch das Markenimage besser sein als in einer anderen Gruppe. Der statistische Zusammenhang zwischen der wahrgenommenen Qualität und der Zufriedenheit kann dann ebenso auf einen Einfluss des Images auf diese beiden Variablen zurückzuführen sein.

 

 

Um die Gruppen vergleichbar zu machen, sind solche „störenden“ Variablen zu kontrollieren. Wenn Daten zu einem einzigen Zeitpunkt erhoben werden (Querschnittsdaten), ist die Regressionsanalyse eine mögliche Methode. Werden alle Störvariablen, die die Ursache und die Wirkung beeinflussen, mit in den Regressionsansatz aufgenommen, wird deren Einfluss auf die beiden interessierenden Variablen herausgerechnet. Strukturgleichungsmodelle (häufig selbst als Kausalanalysen bezeichnet) stellen eine Erweiterung der Regressionsanalyse für die Analyse komplexerer kausaler Zusammenhänge mit mehreren abhängigen Variablen dar.

Bei Querschnittsdaten kann die zeitliche Asymmetrie von Ursache und Wirkung nur durch eine entsprechende Annahme als erfüllt angesehen werden. Des Weiteren ist die Kontrolle unbeobachteter Störvariablen ausgeschlossen. Liegen Längsschnittdaten aus einem Panel vor, können diese Einschränkungen unter der Annahme der Konstanz der unbeobachteten Variablen und ihrer Einflüsse mit Fixed-Effect-Modellen überwunden werden.

Beitrag aus planung&analyse 13/1 in der Rubrik „Statistik kompakt“

 

Autoreninformation

Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.

Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.

 

Literatur

Agresti, A.; Finlay, B.: Introduction to Multivariate Relationships. In: Statistical Methods for the Social Sciences, Upper Saddle River, 2009, S. 301-315.

Legewie, J.: Die Schätzung von kausalen Effekten: Überlegungen zu Methoden der Kausalanalyse anhand von Kontexteffekten in der Schule. In: Kölner Zeitschrift für Soziologie und Sozialpsychologie, Jg. 64/2012, Heft 1, S. 123-153.

Opp, K.-D.: Kausalität als Gegenstand der Sozialwissenschaften und der multivariaten Statistik. In: Wolf, C.; Best, H.: Handbuch der sozialwissenschaftlichen Datenanalyse, Wiesbaden, 2010, S. 9-38.

 
<

---

Share