Multidimensionale Skalierung
Johannes Lüken / Dr. Heiko Schimmelpfennig
Die Multidimensionale Skalierung (MDS) wird vor allem zur Visualisierung der Zusammenhänge zwischen Objekten und/oder Merkmalen eingesetzt. Zumeist ist das Ziel eine zwei-dimensionale Darstellung beispielsweise verschiedener Marken, in der die Marken umso näher beieinander liegen (sollen), je ähnlicher sie wahrgenommen werden.
Einführendes Beispiel
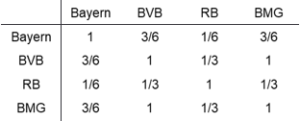
Es wird untersucht, wie ähnlich das Sportangebot der vier deutschen Teilnehmer an der Fußball Champions League in der Saison 2020/21 ist. Neben Fußball bietet Bayern München Basketball, Handball, Kegeln, Schach und Tischtennis an. Bei Borussia Dortmund und Borussia Mönchengladbach werden auch Handball und Tischtennis gespielt. RB Leipzig ist ein reiner Fußballverein. Abbildung 1a zeigt für jeden paarweisen Vergleich den Anteil der Sportarten, den beide Vereine anbieten, an der Anzahl Sportarten, die zumindest bei einem der beiden möglich ist.
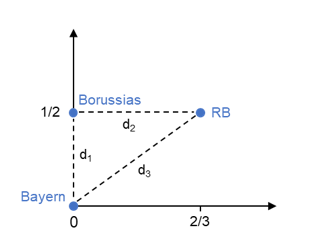 Abbildung 1c: Konfiguration
Abbildung 1c: Konfiguration
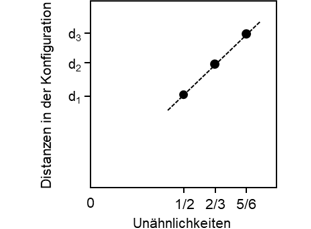
Abbildung 1d: Shepard-Diagramm
Da das Angebot von Borussia Dortmund und Borussia Mönchengladbach identisch ist, werden beide zu einem Objekt „Borussias“ zusammengefasst. Die Ähnlichkeiten werden durch Subtraktion von eins in Unähnlichkeiten transformiert (Abbildung 1b).
Um eine Konfiguration der drei Objekte im zwei-dimensionalen Raum zu erhalten, kann beispielsweise Bayern München zuerst beliebig positioniert werden. Es gelingt, dann die „Borussias“ und schließlich RB Leipzig exakt entsprechend ihrer Unähnlichkeiten zueinander darzustellen (Abbildung 1c). Die Konfiguration ist abgesehen von einer Drehung eindeutig. Werden die Unähnlichkeiten und die Distanzen in der Konfiguration gegeneinander abgetragen, so liegen sie genau auf einer Geraden (Abbildung 1d). Der Korrelationskoeffizient als ein Maß für die Güte der Darstellung ist somit gleich eins.
Drei Objekte lassen sich immer perfekt in einer Ebene abbilden. Bei mehreren Objekten ist dies kaum möglich. Hätten die „Borussias“ unterschiedliche Angebote, wären vier Objekte zu positionieren. Bereits dann wäre es nicht mehr so einfach, die bestmögliche Konfiguration zu finden.
Algorithmen zur Bestimmung einer Konfiguration
Wenn die direkt erhobenen oder berechneten Unähnlichkeiten euklidische Distanzen sind, kann eine Lösung algebraisch ermittelt werden, die ausgehend von der Unähnlichkeitsmatrix ähnlich wie in der Hauptkomponentenanalyse Eigenwerte und -vektoren nutzt, um eine Konfiguration zu bestimmen. Dieses Vorgehen wird häufig als „Klassische MDS“ bezeichnet.
Iterative Algorithmen sind auch bei anderer Skalierung der Un-/Ähnlichkeiten einsetzbar. Im Mittelpunkt steht die Bestimmung von Disparitäten. Eine ordinale MDS strebt an, dass nur die Reihenfolge der Distanzen in der Konfiguration der der Unähnlichkeiten entspricht. Weichen sie voneinander ab, so sind die Disparitäten die bestmögliche Approximation an die Distanzen in der Konfiguration, die der Reihenfolge der Unähnlichkeiten nicht widerspricht (Abbildung 2). Sie werden durch eine monotone Regression bestimmt. Ein alternatives Modell ist die Intervall-MDS. Dort erfolgt die Anpassung durch eine Lineare Regression.
Mittels der quadrierten Abweichungen zwischen Disparitäten und Distanzen wird die Güte einer MDS-Konfiguration quantifiziert. Entsprechende Maße werden als STRESS bezeichnet. Es gibt verschiedene Varianten, die sich in der Art der Normierung unterscheiden. Eine perfekte Abbildung hat einen Stresswert von null.
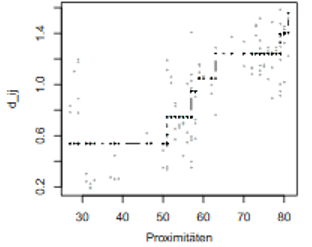
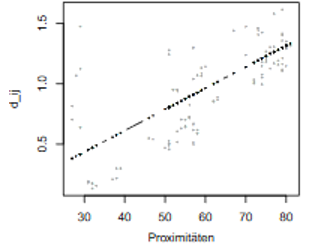
Abbildung 2: Ordinale MDS (links) und Intervall-MDS (rechts)
Ausgehend von einer Startkonfiguartion bestimmt der Algorithmus im Wechsel die Disparitäten und eine neue Konfiguration so, dass sich der STRESS schrittweise verringert bis ein Abbruchkriterium erfüllt ist.
Borg et al. (2010) empfehlen, zumeist ordinale MDS sowie Intervall-MDS durchzuführen und miteinander zu vergleichen. Dabei ist zu berücksichtigen, dass die Intervall-MDS gewöhnlich zu höheren Stresswerten führt als die ordinale MDS, weil sie das restriktivere Modell ist.
Beitrag aus planung&analyse 21/1 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Borg, I., Groenen, P.J.F., Mair, P.: Multidimensionale Skalierung, München und Mering, 2010
<