
Hauptkomponentenanalyse
Johannes Lüken / Dr. Heiko Schimmelpfennig
Die Hauptkomponentenanalyse zählt zu den bedeutendsten Verfahren der Faktorenanalyse. Anhand eines beinahe aktuellen Beispiels wird gezeigt, was eine Hauptkomponente ausmacht und wie sie bestimmt wird.
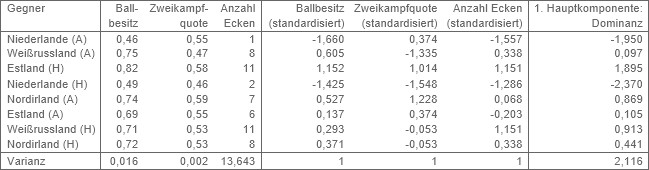
Abbildung: Daten der Qualifikationsspiele der deutschen Nationalmannschaft zur Fußball-EM 2020/21
Grundidee einer Hauptkomponente
Die Tabelle enthält ausgewählte Daten der Qualifikationsspiele der deutschen Fußball-Nationalmannschaft zur EM 2020/21. Ballbesitz, Zweikampfquote und Anzahl Ecken sollen – wenn möglich – zu einem Merkmal „Dominanz“ zusammengefasst werden. Da die Ecken auf einer anderen Skala als die anderen beiden Variablen erhoben werden, bietet sich zunächst eine Standardisierung an. Anschließend wird die Dominanz durch einen gewichteten Mittelwert bestimmt:
Dominanz = a1 ∙ Ballbesitz (standardisiert) + a2 ∙ Zweikampfquote (standardisiert) + a3 ∙ Anzahl Ecken (standardisiert)
Ballbesitz variiert deutlich mehr als Zweikampfquote, das heißt differenziert besser zwischen den Spielen (allgemein zwischen den Fällen). Daraus leitet sich das Ziel ab, die Gewichte a1, a2 und a3 so zu bestimmen, dass die Werte der Dominanz möglichst große Varianz aufweisen. Allerdings steigt die Varianz grundsätzlich mit höheren Gewichten an, da die Beträge der resultierenden Werte dadurch zwangsläufig größer werden. Insofern ist eine Normierung erforderlich. Üblicherweise wird gefordert, dass die Summe der quadrierten Gewichte gleich eins ist.
Extraktion der Hauptkomponenten
Die Varianz der Dominanz kann auch mithilfe der Korrelationsmatrix der drei Variablen berechnet werden. Sie ist gleich
Die Gewichte a1, a2 und a3 sind folglich so zu bestimmen, dass dieses Produkt maximal wird. Unter der Nebenbedingung a1² + a2² + a3² = 1 führt die Optimierungsaufgabe zu einem Eigenwertproblem. Der Eigenvektor zu dem größten Eigenwert der Korrelationsmatrix ist die erste Hauptkomponente und entspricht den gesuchten Gewichten. Diese sind a1 = 0,659, a2 = 0,389 und a3 = 0,644. Der Eigenwert 2,116 selbst ist gleich der Varianz der Werte der Dominanz, die der letzten Spalte der Tabelle zu entnehmen sind. Die Dominanz der deutschen Fußballnationalmannschaft war im Heimspiel gegen Estland am höchsten und in den beiden Spielen gegen die Niederlande am geringsten. Der durch die erste extrahierte Hauptkomponente erklärte Anteil der Varianz der drei Variablen beträgt 2,116 / 3 = 70,5 %.
Die Korrelation zwischen den Werten einer Variable und denen der Hauptkomponente kennzeichnet die Ladung der Variable auf die Hauptkomponente. Diese ist für den Ballbesitz gleich 0,958, für die Zweikampfquote gleich 0,566 und für die Anzahl Ecken gleich 0,936. In den Ladungen spiegelt sich die hohe Korrelation zwischen Ballbesitz und Anzahl Ecken wider. Beide laden höher als die Zweikampfquote auf die erste Hauptkomponente. Dennoch ist die Ladung der Zweikampfquote hoch genug, dass auch sie zu dieser Hauptkomponente gehört und mit zur Dominanz beiträgt – wenn auch etwas weniger als die anderen beiden Variablen.
Prinzipiell können so viele Hauptkomponenten extrahiert werden, wie beobachtete Variablen in die Analyse eingehen. Die weiteren Hauptkomponenten werden sukzessive so bestimmt, dass sie möglichst viel von der noch nicht erklärten Varianz erklären und orthogonal zu den übrigen Hauptkomponenten sind, das heißt die Werte der Hauptkomponenten nicht miteinander korrelieren.
Beitrag aus planung&analyse 20/2 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Handl, A.: Multivariate Analysemethoden, 2. Auflage, Berlin, Heidelberg, 2010, S. 115-147.
Passend dazu:
<








