Einführung in die Faktorenanalyse
Johannes Lüken / Dr. Heiko Schimmelpfennig
Die Faktorenanalyse ist ein Sammelbegriff für verschiedene Verfahren, denen das Ziel gemein ist, Gruppen von beobachteten Variablen zu identifizieren, die untereinander stark zusammenhängen, beziehungsweise Vermutungen über die Zusammenhänge dieser Variablen zu überprüfen.
Übersicht der Verfahren
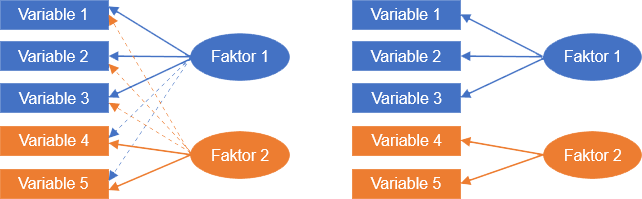
Grundsätzlich wird zwischen der explorativen und der konfirmatorischen Faktorenanalyse unterschieden. Die explorative Faktorenanalyse dient dazu, aus einer Menge von beobachteten Variablen, „künstliche“ Variablen zu konstruieren, die jeweils möglichst mit mehreren der beobachteten Variablen hoch und mit den anderen kaum korrelieren. Diese „künstliche“ (theoretische) Variable wird als Faktor bezeichnet, die Korrelationen als Faktorladungen. Bei der konfirmatorischen Faktorenanalyse wird dagegen vorgegeben, welche beobachtete Variable mit welchem Faktor stark zusammenhängt. Anschließend wird überprüft, inwiefern sich unter Berücksichtigung dieser vermuteten Struktur die Korrelationen beziehungsweise Kovarianzen der beobachteten Variablen reproduzieren lassen. Die Abbildung veranschaulicht den Unterschied. Zudem verdeutlicht die Richtung der Pfeile, dass die Faktoren Erklärungen der Ausprägungen der beobachteten Variablen sein sollen.
Abbildung: Explorative (links) und konfirmatorische (rechts) Faktorenanalyse
Innerhalb der explorativen Faktorenanalyse sind die Hauptkomponentenanalyse und das Modell gemeinsamer Faktoren die bedeutendsten Verfahren. Ihr Unterschied lässt sich an der Varianz einer beobachteten Variablen festmachen. Diese setzt sich zusammen aus der Varianz, die eine Variable mit den anderen beteiligten Variablen gemeinsam hat, und der, die sie mit keiner anderen Variable teilt. In der Hauptkomponentenanalyse sollen die Faktoren – eigentlich die Hauptkomponenten – die gesamte Varianz der beobachteten Variablen erklären. Das Modell gemeinsamer Faktoren möchte nur die gemeinsame Varianz erklären.
Anwendungsbereiche
Datenreduktion: Für jeden Faktor können individuelle Werte – die Faktorwerte – bestimmt werden, die die Ausprägung eines Faktors bei einem Untersuchungsobjekt wiedergeben. Weniger Faktoren als Variablen bedeuten eine geringere Anzahl an Werten je Fall. Ist der durch die zumeist mit einer Hauptkomponentanalyse extrahierten Faktoren erklärte Anteil der Varianz der Variablen hoch genug, können Tabellen oder Diagramme mit Faktorwerten komprimierter und damit übersichtlicher dargestellt werden oder die Faktorwerte Input anderer multivariater Verfahren wie zum Beispiel einer Clusteranalyse sein. Werden nicht mehr als drei Faktoren extrahiert, ist ein Mapping der Fälle im durch die Faktoren aufgespannten zwei- oder dreidimensionalen Raum möglich.
Vermeiden von Redundanz: Aus den Variablen, die zu einer Gruppe zusammengefasst werden, weil sie mit einem Faktor hoch korrelieren, können eine oder mehrere ausgewählt werden, um in weiteren Untersuchungen Redundanz und Erhebungsaufwand zu reduzieren.
Regressionsanalyse: Grundlegend für valide Ergebnisse einer Regressionsanalyse sind allenfalls schwach korrelierende unabhängige Variablen. Werden Faktoren als unabhängige Variablen genutzt ist diese Voraussetzung erfüllt, da Faktoren im Allgemeinen so extrahiert werden, dass sie nicht miteinander korrelieren. Unterscheiden lassen sich zwei Varianten: die Anzahl der Faktoren ist geringer (Faktorregression) oder gleich (Orthogonalisierung) der Anzahl der ursprünglichen beobachteten Variablen. Vorwiegend eingesetzt wird zu diesem Zweck die Hauptkomponentenanalyse.
Überprüfen von Messmodellen: Cronbachs Alpha ist ein gängiges Maß zur Beurteilung der Güte von Multi-Item-Skalen. Exploratorische und konfirmatorische Faktorenanalyse liefern weitere Maße und ermöglichen die Überprüfung, ob ein Konstrukt ein- oder mehrdimensional ist.
Beitrag aus planung&analyse 20/1 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Wolff, H.-G., Bacher, J.: Hauptkomponentenanalyse und explorative Faktorenanalyse. In: Wolf, C., Best, H. (Hrsg.): Handbuch der sozialwissenschaftlichen Datenanalyse, Wiesbaden, 2010, S. 333-365.
Passend dazu:
<