Einfaktorielle Varianzanalyse
Johannes Lüken / Dr. Heiko Schimmelpfennig
Mit der einfaktoriellen Varianzanalyse wird überprüft, ob sich die Mittelwerte eines metrischen Merkmals zwischen drei oder mehr Gruppen signifikant voneinander unterscheiden. Die Gruppen stellen die Ausprägungen beziehungsweise Stufen des Faktors dar, dessen Einfluss auf die metrische Variable untersucht wird.
Multiple t-Tests
Es soll herausgefunden werden, ob die Kaufbereitschaft für ein Produkt von der Verpackung abhängt. Zur Auswahl stehen beispielsweise drei verschiedene Verpackungen. Die Probanden bekommen zufällig eine davon gezeigt und werden nach ihrer Kaufbereitschaft gefragt. Wenn sich die mittlere Kaufbereitschaft zwischen mindestens zwei Verpackungen signifikant unterscheidet, besitzt die Verpackung einen Einfluss auf die Kaufbereitschaft. Mittels statistischem Test ist somit die Hypothese zu überprüfen, ob die Mittelwerte der Kaufbereitschaft für alle drei Verpackungen gleich sind. Mit einem t-Test kann nur die Hypothese untersucht werden, ob zwei Mittelwerte gleich sind. Insofern wären in diesem Beispiel drei t-Tests durchzuführen, um alle möglichen paarweisen Vergleiche abzudecken.
Ein hierfür verwendetes Signifikanzniveau α gilt jedoch nicht mehr für die übergreifende Hypothese, dass alle drei Mittelwerte gleich sind. Infolge der α-Fehler-Kumulierung erhöht sich dieses auf 1 – (1 – α)m mit m = Anzahl der t-Tests = ½ ∙ (Anzahl Faktorstufen) ∙ (Anzahl Faktorstufen – 1). Um die eigentliche Hypothese zu überprüfen, ist demnach nicht nur die mehrfache Durchführung eines t-Tests erforderlich, sondern zusätzlich das Signifikanzniveau für einen einzelnen Test in Abhängigkeit der Anzahl der Faktorstufen anzupassen:
Angepasstes Signifikanzniveau = 1 – (1 – α)1/m
Vereinfachend kann auch die Bonferroni-Korrektur α/m verwendet werden. In dem Beispiel wäre somit bei jedem einzelnen Test ein Signifikanzniveau von lediglich α = 1,7% vorzugeben, um insgesamt ein Signifinkanzniveau von 5% einzuhalten.

Grundidee der Varianzanalyse: Streuungszerlegung
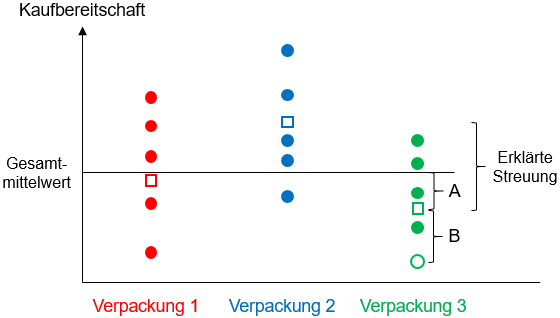
Die Varianzanalyse ermöglicht ein einfacheres Vorgehen, um die Hypothese zu überprüfen, dass die Mittelwerte in mehreren Gruppen gleich sind. Sie weist zudem eine höhere Power als multiple t-Tests auf, da ein einzelner t-Test niemals die gesamte Stichprobe nutzt. Die Abbildung zeigt beispielhaft einen Teil der erhobenen individuellen Kaufbereitschaften für drei verschiedene Verpackungen. Die Abweichung eines Messwerts ¡ vom Gesamtmittelwert lässt sich aufteilen in die Abweichung A des Mittelwerts der Messwerte für eine Verpackung – des Gruppenmittelwerts ¨ – vom Gesamtmittelwert und die Abweichung B des Messwerts vom Gruppenmittelwert.
Die Abweichungen der Gruppenmittelwerte vom Gesamtmittelwert können auf die unterschiedlichen Verpackungen zurückgeführt werden. Insofern kann ihre Streuung durch den betrachteten Faktor erklärt werden. Die Abweichungen der Messwerte einer Gruppe von dem Gruppenmittelwert sind auf andere nicht berücksichtigte Einflüsse zurückzuführen. Diese Streuung ist damit nicht zu erklären.
Abbildung: Aufteilung der Abweichung eines Messwerts vom Gesamtmittelwert
Signifikanztest und Effektstärke
Ob Unterschiede zwischen den Gruppenmittelwerten in einer Stichprobe nicht allein zufällig aufgetreten sind, wird in der einfaktoriellen Varianzanalyse mit einem Signifikanztest überprüft. Ist die durch den Faktor erklärte Streuung deutlich größer als die nicht erklärte Streuung spricht dies gegen die Hypothese, dass alle Gruppenmittelwerte gleich sind, und somit in dem Beispiel für einen Einfluss der Verpackung auf die Kaufbereitschaft. Durch das vorgegebene Signifikanzniveau ist bestimmt, wie groß die erklärte im Verhältnis zur nicht erklärten Streuung mindestens sein muss, damit die Hypothese abgelehnt wird.
Ob ein so als statistisch signifikant identifizierter Einfluss auch relevant ist, lässt sich anhand der Effektstärke beurteilen. Diese ist definiert als Anteil der erklärten Streuung an der gesamten Streuung aller Messwerte. Nach Cohen (1988) ist in der Varianzanalyse ein Effekt ab 0,01 klein, ab 0,06 mittel und ab 0,14 groß.
Interessiert bei einem signifikanten Ergebnis, für welche Faktorstufen sich die Mittelwerte signifikant unterscheiden, sind entweder doch einzelne t-Tests mit angepasstem Signifikanzniveau oder Post-hoc-Tests wie der Scheffé-Test durchzuführen.
Beitrag aus planung&analyse 17/2 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Cohen, J.: Statistical Power Analysis for the Behavioral Sciences, 2. Auflage, Hillsdale, 1988.
Rasch, B.; Friese, M.; Hofmann, W.; Naumann, E.: Einfaktorielle Varianzanalyse. In: Quantitative Methoden 2, 4. Auflage, Berlin, Heidelberg, 2014, S. 1-34.
<