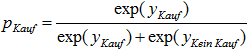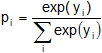Discrete Choice Modelle
Johannes Lüken / Dr. Heiko Schimmelpfennig
Eine bedeutende Aufgabenstellung der Marktforschung ist die Bestimmung der maßgeblichen Einflüsse auf Kaufentscheidungen. Die zu erklärende Variable bildet die Entscheidung ab und ist somit kategorial. Zur Analyse derartiger diskreter Auswahlsituationen kommen häufig Logit-Modelle zum Einsatz.
Binäres Logit-Modell
Im einfachsten Fall stehen zwei Alternativen zur Auswahl. Beispielsweise könnte interessieren, was die Entscheidung für oder gegen den Kauf eines Produktes bestimmt. Abbildung 1 zeigt einen Ausschnitt aus einer möglichen Datenbasis, um die Einflüsse von Alter, Einkommen und Haushaltsgröße auf die Kaufentscheidung zu untersuchen.
 Abbildung 1: Daten für ein binäres Logit-Modell
Abbildung 1: Daten für ein binäres Logit-Modell
Die Grundidee eines Logit-Modells ist, auf Basis der unabhängigen Variablen, die metrisch und/oder kategorial sein können, die Wahrscheinlichkeit zu schätzen, dass eine Alternative ausgewählt wird. Dazu werden für jede der beiden Alternativen „Kauf“ und „ Kein Kauf“ die Werte der unabhängigen Variablen wie in einem linearen Regressionsansatz mit Regressionskoeffizienten gewichtet und zu einem Wert zusammengefasst. Zu jeder Alternative gehört ein eigenes Set von Koeffizienten. Für die Alternative „Kauf“ ist somit
Die Wahrscheinlichkeit, dass das Produkt gekauft wird, ist dann
und dementsprechend die Wahrscheinlichkeit, dass es nicht gekauft wird, 1 – pKauf. Zur Schätzung des Modells werden alle Regressionskoeffizienten einer Alternative – zum Beispiel die für „Kein Kauf“ – auf 0 gesetzt und die Koeffizienten der Alternative „Kauf“ mittels Maximum-Likelihood-Schätzung bestimmt.
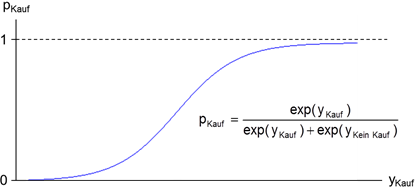
Abbildung 2 veranschaulicht den sich aus der Berechnung ergebenden typischen logistischen Funktionsverlauf der Auswahl- bzw. Kaufwahrscheinlichkeit. Im Gegensatz zu einer linearen Regression ist für die Veränderung der abhängigen Variable – der Wahrscheinlichkeit – infolge der Änderung einer unabhängigen Variable entscheidend, wo man sich auf der Kurve befindet, das heißt welche konkreten Werte die unabhängigen Variablen aufweisen. Dennoch ermöglichen geeignete Tests wie der Likelihood-Ratio-Test die Bestimmung der Signifikanz der Einflussgrößen.
Abbildung 2: Logistische Funktion der Auswahlwahrscheinlichkeit
Multinomiales Logit-Modell
Ein Multinomiales Logit-Modell (MNL-Modell) stellt die Verallgemeinerung des binären Logit-Modells auf mehr als zwei zur Auswahl stehende Alternativen dar, um zum Beispiel die Auswahlentscheidung zwischen mehreren Produkten abzubilden. Wie im binären Logit-Modell sind die unabhängigen Variablen Merkmale der Befragten wie Einkommen oder Alter, die über die Befragten hinweg variieren, aber für alle Alternativen gleich sind. Für jede Alternative i werden eigene Regressionskoeffizienten geschätzt, auf Basis derer wiederum Auswahlwahrscheinlichkeiten berechnet werden können:
Conditional Logit-Modell
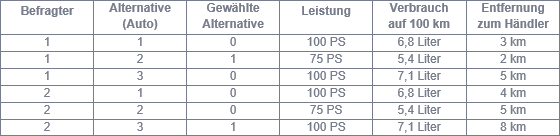
Soll nicht nur der Einfluss von Merkmalen der Befragten, sondern auch der von Merkmalen der Alternativen auf die Entscheidung untersucht werden, ist das Conditional Logit-Modell zu verwenden. Abbildung 3 zeigt einen Ausschnitt aus einer Datenbasis zur Analyse des Einflusses von Leistung, Verbrauch und Entfernung zum Händler auf die Wahl eines Autos. Die Merkmale variieren entweder nur über die Alternativen (Leistung, Verbrauch) oder über Alternativen und Befragte (Entfernung).
Abbildung 3: Daten für ein Conditional Logit-Modell
Entsprechend der Anzahl der Alternativen liegen für jeden Befragten mehrere – in diesem Beispiel drei – Datensätze vor. Eine Dummy-Variable (Gewählte Alternative) gibt dann die Entscheidung des Befragten an. Beispielsweise hat der Befragte 1 das Auto 2 ausgewählt. Im Gegensatz zum MNL-Modell wird je Variable nicht für alle Alternativen ein eigener, sondern ein für alle Alternativen gleicher Regressionskoeffizient geschätzt. Die Berechnung der Auswahlwahrscheinlichkeiten erfolgt analog zum MNL-Modell. Darüber hinaus erlaubt das Conditional Logit-Modell auch, Merkmale der Befragten wie das Einkommen, deren Ausprägungen für alle Alternativen gleich sind, zu berücksichtigen.
Beitrag aus planung&analyse 13/6 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Cameron, A. C.; Trivedi, P. K.: Multinomial Models, In: Microeconometrics, Cambridge et al., 2005, S. 490-503.
Maddala, G. S.: Discrete Regression Models, In: Limited-Dependent and Qualitative Variables in Econometrics, Cambridge et al., 1983, S. 13-46.
<