
Bestimmung und Darstellung von Faktorwerten
Johannes Lüken / Dr. Heiko Schimmelpfennig
Für jeden Faktor können innerhalb einer Hauptkomponentenanalyse individuelle Faktorwerte bestimmt werden, die die Ausprägung eines Faktors bei einem Untersuchungsobjekt wiedergeben. Damit lassen sich Tabellen oder Diagramme übersichtlicher als mit einer Vielzahl an Variablen erstellen.
Bestimmung der Faktorwerte
Die Faktorwerte ergeben sich als gewichteter Mittelwert der standardisierten Werte der in eine Hauptkomponentenanalyse eingehenden Variablen. Die Gewichte unterscheiden sich zwischen den Faktoren. Die Faktorwerte sind zentriert und besitzen eine Varianz, die den Eigenwerten der Korrelationsmatrix entspricht, oder sind standardisiert wie z.B. in SPSS, indem durch die Standardabweichung – die Wurzel aus dem jeweiligen Eigenwert – dividiert wird. In rotierten Lösungen stimmen Varianzen und Eigenwerte zwar nicht mehr überein, zentriert bzw. standardisiert sind sie aber nach wie vor.
Die Abbildung 1 zeigt zum einen die rotierte Faktorladungsmatrix einer Hauptkomponentenanalyse, mit der sieben Merkmale zur Zufriedenheit von Strandurlaubern auf zwei Faktoren reduziert werden (Lüken/Schimmelpfennig 2020). Die Merkmale wurden auf einer 5er-Ratingskala erhoben, auf der größere Werte eine höhere Zufriedenheit bedeuten. Der erste Faktor repräsentiert die Zufriedenheit mit den sonstigen Aktivitäten in einem Strandurlaub, der zweite Faktor die Zufriedenheit mit den Bedingungen für Strandaktivitäten. Zum anderen ist in Abbildung 1 die Koeffizientenmtarix dargestellt, die die Gewichte enthält, mit denen die standardisierten Werte der sieben Variablen multipliziert und somit zu den Faktorwerten zusammengefasst werden. Bezeichnet A die Faktorladungsmatrix, so ergibt sich die Koeffizienenmatrix durch die Matrizenmultiplikation A∙(A‘∙A)-1.
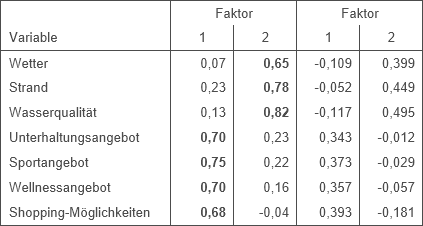
Abbildung 1: Faktorladungs- und Koeffizientenmatrix nach Varimax-Rotation
Interpretation der Faktorwerte
Der Übersicht halber sind in Abbildung 2.1 nur die Faktorwerte der Teilgruppe von 31 Alleinreisenden in der Stichprobe dargestellt. Jeder Fall kann in Relation zur Gesamtstichprobe interpretiert werden. Ist ein Faktorwert größer (kleiner) als 0, ist er hinsichtlich dieser Dimension zufriedener (weniger zufrieden) als der Durchschnitt aller 359 analysierten Strandurlauber.
Nicht abgelesen werden kann das Niveau der Zufriedenheit sowohl der Gesamtstichprobe als auch jeden einzelnen Falls. Um die Faktorwerte diesbezüglich einordnen zu können, ist die Bestimmung ihrer Minima und Maxima notwendig. Für das Maximum (Minimum) sind die positiven (negativen) Koeffizienten mit dem größt- (kleinst-) möglichen standardisierten Wert, die negativen (positiven) Koeffizienten mit dem kleinst- (größt-) möglichen standardisierten Wert zu multiplizieren. In diesem Beispiel ist das Maximum des ersten Faktors 3,16 und des zweiten Faktors 1,85. Das jeweilge Minimum beträgt -3,44 bzw. -4,81. Zu beachten ist aber, dass ein Fall z.B. das Maximum beider Faktoren niemals tatsächlich aufweisen kann. Dazu müsste er unter anderem beim Wetter einerseits mit 1, andererseits mit 5 geantwortet haben. Dennoch vermittelt die grafische Darstellung einen Eindruck von der Höhe der Zufriedenheit, wenn Maxima und Minima die Grenzen der Diagrammfläche wie in Abbildung 2.2 definieren. Ferner wäre damit eine Transformation der Faktorwerte auf eine Skala mit gängigeren Grenzwerten möglich.
Wenn einzelne Fälle nicht dargestellt werden können, weil es zu viele sind, können Teilgruppen in einem Streudiagramm durch ihre Zentroide repräsentiert werden. In allen Abbildungen ist der rote Punkt der Zentroid der Gruppe der Alleinreisenden. Werden mehr als zwei Faktoren extrahiert, ist ein Netzdiagramm anstelle eines Streudiagramms nützlich.
Alternative Bestimmung von Faktorwerten
Eine weitere Möglichkeit zur Bestimmung von Faktorwerten insbesondere bei gleichskalierten Variablen ist die Berechnung des Mittelwerts über die ursprünglichen Werte nur der Variablen, die jeweils einem Faktor gemäß Ladungsmatrix zugeordnet werden. Ein Vorteil ist, dass sich die Faktorwerte unmittelbar auf der ursprünglichen Skala interpretieren lassen. Eine entsprechende Darstellung zeigt Abbildung 2.3. Bei negativen Faktorladungen wäre zuvor ein „Umpolen“ notwendig. Gegebenenfalls können die Faktorladungen zur Berechung eines gewichteten Mittelwerts herangezogen werden.
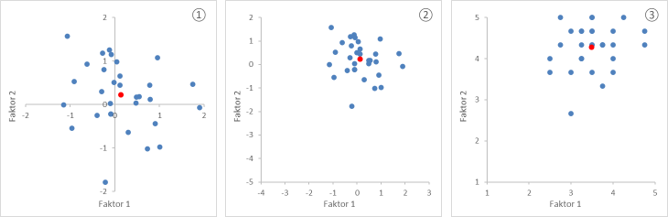
Abbildung 2: Streudiagramme der Faktorwerte
Beitrag aus planung&analyse 20/4 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Lüken, J.; Schimmelpfennig, H: Hauptkomponentenanalyse zur Datenreduktion. In: planung&analyse, Nr. 3/2020, S. 19.
<






