Bedeutung der Effektstärke
Johannes Lüken / Dr. Heiko Schimmelpfennig
Ein signifikantes Ergebnis eines statistischen Tests wird häufig gleich gesetzt mit hoher Relevanz zum Beispiel für Entscheidungen. Diese Gleichung geht jedoch aufgrund der Abhängigkeit der Signifikanz vom Stichprobenumfang nicht ohne weiteres auf. Zur Beurteilung der Relevanz eines Ergebnisses sollte deshalb mit der Effektstärke ein weiteres Maß herangezogen werden.
Statistische Signifikanz vs. Relevanz
Was bedeutet statistisch signifikant? Wir gehen davon aus, dass ein Effekt – ein Unterschied zwischen zwei Gruppen oder ein Zusammenhang zwischen zwei Variablen – nicht nur zufällig in einer Stichprobe zu beobachten ist, sondern fast sicher auch in der Grundgesamtheit existiert. Nur mit einer geringen Wahrscheinlichkeit (meistens wählt man eine Irrtumswahrscheinlichkeit von 5%) liegen wir falsch. Über das Ausmaß des Effekts, zum Beispiel die Höhe der Differenz zwischen zwei Mittelwerten, sagt der Test nichts aus. Selbst ein sehr kleiner Unterschied wird als statistisch signifikant interpretiert, wenn man nur den Stichprobenumfang groß genug wählt. Aber ist ein statistisch signifikanter Unterschied von beispielweise 0,03 auf einer 7-stufigen Ratingskala tatsächlich bedeutsam im Sinne von praktisch relevant?
Relative Effektstärke
Ein Maß für die praktische Relevanz ist die relative Effektstärke. Für den Vergleich der Mittelwerte 
und 
von zwei unabhängigen Stichproben wird die Mittelwertdifferenz an der gemeinsamen Standardabweichung s standardisiert:
s ergibt sich aus den mit den Teilstichprobenumfängen gewichteten Standardabweichungen innerhalb der Teilstichproben. Dennoch ist die relative Effektstärke kaum abhängig vom Stichprobenumfang. Durch die Standardisierung wird zudem der Einfluss der zugrunde liegenden Skala herausgerechnet. Somit ist anhand der relativen Effektstärke der Vergleich von Untersuchungsergebnissen möglich, denen unterschiedliche Stichprobenumfänge und/oder Erhebungsinstrumente zugrunde liegen. Ferner lassen sich generell anwendbare Referenzwerte zur Klassifikation der Effektstärke angeben. Etabliert hat sich, einen absoluten Effekt |d| ab 0,2 als klein, ab 0,5 als mittel und ab 0,8 als groß zu bezeichnen.
Weitere Maße der Effektstärke
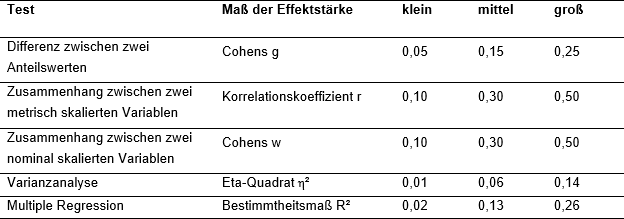
Die relative Effektstärke ist nicht nur für den Vergleich von Mittelwerten, sondern auch für viele weitere Tests definiert. Die Abbildung gibt einen Überblick über geläufige Maße sowie ihre Grenzwerte zur Klassifikation der Effektstärke nach Cohen (1988).
Abbildung: Maße der Effektstärke
Hypothesen(um)formulierung
Üblicherweise wird beim Mittelwertvergleich die Hypothese getestet, dass sich die Mittelwerte in den Grundgesamtheiten nicht unterscheiden, das heißt ihre Differenz Null ist. Ablehnen der Hypothese bedeutet, dass sich beide Mittelwerte signifikant voneinander unterscheiden. Signifikante Unterschiede können dann anhand der Effektstärke genauer betrachtet werden.
Alternativ wird vorgeschlagen, stattdessen die Hypothese zu überprüfen, dass die Differenz in der Grundgesamtheit die für die zugrunde liegende Fragestellung als relevant erachtete Differenz nicht überschreitet. Gelten auf der zu Beginn genannten Ratingskala beispielsweise Differenzen von 0,5 als relevant, so wäre die Hypothese zu testen, dass die Differenz > 0,5 ist. Ablehnen der Hypothese bedeutet dann, dass sich die beiden Mittelwerte mindestens um die Differenz von 0,5 signifikant voneinander unterscheiden. Somit ist ein Effekt, der in diesem Sinne statistisch signifikant ist, immer zugleich auch praktisch relevant. Für die anderen Tests kann die Anpassung der Hypothese analog erfolgen.
Beitrag aus planung&analyse 16/3 in der Rubrik „Statistik kompakt“
Autoreninformation
Johannes Lüken war bis 2021 Leiter des Bereichs Multivariate Analysen bei IfaD.
Prof. Dr. Heiko Schimmelpfennig ist Projektleiter im Bereich Data Science bei IfaD sowie seit Oktober 2021 als Professor für Forschungsmethoden an der BSP Business & Law School Hamburg tätig. Zuvor war er sieben Jahre Professor für Betriebswirtschaft und Studiengangsleiter an der University of Applied Sciences Europe. Er ist bei IfaD schwerpunktmäßig für die Beratung, Anwendung und Schulung von Multivariaten Verfahren verantwortlich und vertritt in der Lehre das Gebiet der Quantitativen Methoden der Wirtschaftswissenschaft.
Literatur
Cohen, J.: Statistical Power Analysis for the Behavioral Sciences, 2. Auflage, Hillsdale, 1988.
Ellis, P.D.: The Essential Guide to Effect Sizes, Cambridge, 2010.
Lind, G.: Effektstärken: Statistische, praktische und theoretische Bedeutsamkeit empirischer Befunde, http://www.uni-konstanz.de/ag-moral/pdf/Lind-2014_Effektstaerke-Vortrag.pdf, 2014.
Quatember, A.: Das Signifikanz-Relevanz-Problem beim statistischen Testen von Hypothesen. In: ZUMA-Nachrichten, Jg. 29/2005, 57, S. 128-150.
<
Share
